a) Cho một vật chuyển động với vận tốc y = v(t) (m/s). Cho 0 < a < b và v(t) > 0 với mọi \(t \in [a;b]\). Hãy giải thích vì sao \(\int\limits_a^b {v(t)dt} \) biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến b (a,b tính theo giây)
b) Áp dụng công thức ở câu a) để giải bài toán sau: một vật chuyển động với vận tốc v(t) = 2 – sint (m/s). Tính quãng đường vật di chuyển trong khoảng thời gian từ thời điểm t = 0 (s) đến thời điểm \(t = \frac{{3\pi }}{4}\) (s)
a) Sử dụng kiến thức đạo hàm của quãng đường là vận tốc
b) Sử dụng định nghĩa tích phân để tính toán
a) Vì vận tốc là đạo hàm của quãng đường nên \(\int\limits_a^b {v(t)dt} = \left. {s(t)} \right|_a^b\)
Do đó \(\int\limits_a^b {v(t)dt} \) biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến b
b) Quãng đường vật di chuyển trong khoảng thời gian đó là:\(s(t) = \int\limits_0^{\frac{{3\pi }}{4}} {v\left( t \right)} dt = \int\limits_0^{\frac{{3\pi }}{4}} {\left( {2--sint} \right)} dt = \left. {\left( {2x + \cos x} \right)} \right|_0^{\frac{{3\pi }}{4}} = \frac{{3\pi }}{2} - \frac{{2 + \sqrt 2 }}{2} \approx 3(m/s)\)
Các bài tập cùng chuyên đề
Tính tích phân \(\int\limits_2^3 {\frac{1}{{{x^2}}}} dx\) có giá trị bằng:
A. \(\frac{1}{6}\)
B. \( - \frac{1}{6}\)
C. \(\frac{{19}}{{648}}\)
D. \( - \frac{{19}}{{648}}\)
Tích phân \(\int\limits_{\frac{\pi }{7}}^{\frac{\pi }{5}} {\sin xdx} \) có giá trị bằng:
Tích phân \(I = \int\limits_0^1 {\frac{{{3^x}}}{2}dx} \) có giá trị bằng:
A. \( - \frac{1}{{\ln 3}}\)
B. \(\frac{1}{{\ln 3}}\)
C. -1
D. 1
Tính:
a) \(\int\limits_0^1 {({x^6} - 4{x^3} + 3{x^2})dx} \)
b) \(\int\limits_1^2 {\frac{1}{{{x^4}}}dx} \)
c) \(\int\limits_1^4 {\frac{1}{{x\sqrt x }}dx} \)
d) \(\int\limits_0^{\frac{\pi }{2}} {(4\sin x + 3\cos x)dx} \)
e) \(\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {{{\cot }^2}xdx} \)
g) \(\int\limits_0^{\frac{\pi }{4}} {{{\tan }^2}xdx} \)
h) \(\int\limits_{ - 1}^0 {{e^{ - x}}dx} \)
i) \(\int\limits_{ - 2}^{ - 1} {{e^{x + 2}}dx} \)
k) \(\int\limits_0^1 {({{3.4}^x} - 5{e^{ - x}})dx} \)
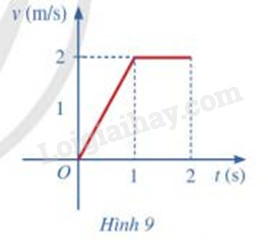
Một vật chuyển động với vận tốc được cho bởi đồ thị ở Hình 9.
a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên
b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên
Ở nhiệt độ \(37^\circ C\), một phản ứng hóa học từ chất đầu A, chuyển hóa thành sản phẩm B theo phương trình: \(A \to B\). Giả sử y(x) là nồng độ chất A (đơn vị mol \({L^{ - 1}}\)) tại thời gian x (giây), y(x) > 0 với \(x \ge 0\), thỏa mãn hệ thức \(y'(x) = - {7.10^{ - 4}}y(x)\) với \(x \ge 0\). Biết rằng tại x = 0, nồng độ (đầu) của A là 0,05 mol \({L^{ - 1}}\).
a) Xét hàm số \(f(x) = \ln y(x)\) với \(x \ge 0\). Hãy tính f’(x), từ đó hãy tìm hàm số f(x)
b) Giả sử tính nồng độ trung bình chất A (đơn vị mol \({L^{ - 1}}\)) từ thời điểm a(giây) đến thời điểm b(giây) với 0 < a < b theo công thức \(\frac{1}{{b - a}}\int\limits_a^b {y(x)dx} \). Xác định nồng độ trung bình của chất A từ thời điểm 15 giây đến thời điểm 30 giây.
Tính các tích phân sau:
a) \(\int\limits_1^2 {{x^4}dx} \)
b) \(\int\limits_1^2 {\frac{1}{{\sqrt x }}dx} \)
c) \(\int\limits_0^{\frac{\pi }{4}} {\frac{1}{{{{\cos }^2}x}}dx} \)
d) \(\int\limits_0^2 {{3^x}dx} \)
Tính các tích phân sau:
a) \(\int\limits_0^1 {{{\left( {1 - 2x} \right)}^2}dx} \);
b) \(\int\limits_1^4 {\frac{{x - 2}}{{\sqrt x }}dx} \).
Tính các tích phân sau:
a) \(\int\limits_0^2 {\left| {2x - 1} \right|dx} \);
b) \(\int\limits_{ - 2}^3 {\left| {x - 1} \right|dx} \).
Tính các tích phân sau:
a) \(\int\limits_0^{\frac{\pi }{2}} {\left( {3\cos x + 2\sin x} \right)dx} \);
b) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{4}} {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} \).
Tính các tích phân sau:
a) \(\int\limits_0^1 {\left( {{3^x} - 2{e^x}} \right)dx} \);
b) \(\int\limits_0^1 {\frac{{{{\left( {{e^x} - 1} \right)}^2}}}{{2{e^x}}}dx} \).
Phát biểu nào sau đây là đúng?
A. \(\int\limits_a^b {\sin xdx} = \sin a - \sin b\).
B. \(\int\limits_a^b {\sin xdx} = \sin b - \sin a\).
C. \(\int\limits_a^b {\sin xdx} = \cos a - \cos b\).
D. \(\int\limits_a^b {\sin xdx} = \cos b - \cos a\).
Phát biểu nào sau đây là đúng? Biết \(f\left( x \right) = \frac{1}{{{{\sin }^2}x}}\) liên tục trên \(\left[ {a;b} \right]\).
A. \(\int\limits_a^b {\frac{1}{{{{\sin }^2}x}}dx} = \cot a - \cot b\).
B. \(\int\limits_a^b {\frac{1}{{{{\sin }^2}x}}dx} = \cot b - \cot a\).
C. \(\int\limits_a^b {\frac{1}{{{{\sin }^2}x}}dx} = \tan a - \tan b\).
D. \(\int\limits_a^b {\frac{1}{{{{\sin }^2}x}}dx} = \tan b - \tan a\).
Tích phân \(\int\limits_1^2 {\frac{{ - 3}}{{{x^3}}}dx} \) có giá trị bằng:
A. \(\frac{9}{8}\).
B. \( - \frac{{45}}{{64}}\).
C. \(\frac{{15}}{8}\).
D. \( - \frac{9}{8}\).
Tích phân \(\int\limits_1^2 {\frac{1}{{x\sqrt x }}dx} \) có giá trị bằng:
A. \(2 - \sqrt 2 \).
B. \(2 + \sqrt 2 \).
C. \(\frac{{ - \sqrt 2 + 8}}{{20}}\).\
D. \(\frac{{ - \sqrt 2 - 8}}{{20}}\).
Phát biểu nào sau đây là đúng?
A. \(\int\limits_a^b {\cos xdx} = \sin a - \sin b\).
B. \(\int\limits_a^b {\cos xdx} = \sin b - \sin a\).
C. \(\int\limits_a^b {\cos xdx} = \cos a - \cos b\).
D. \(\int\limits_a^b {\cos xdx} = \cos b - \cos a\).
Phát biểu nào sau đây là đúng? Biết \(f\left( x \right) = \frac{1}{{{{\cos }^2}x}}\) liên tục trên \(\left[ {a;b} \right]\).
A. \(\int\limits_a^b {\frac{1}{{{{\cos }^2}x}}dx} = \cot a - \cot b\).
B. \(\int\limits_a^b {\frac{1}{{{{\cos }^2}x}}dx} = \cot b - \cot a\).
C. \(\int\limits_a^b {\frac{1}{{{{\cos }^2}x}}dx} = \tan a - \tan b\).
D. \(\int\limits_a^b {\frac{1}{{{{\cos }^2}x}}dx} = \tan b - \tan a\).
Cho \(m\) thoả mãn \(m > 0,m \ne 1\). Phát biểu nào sau đây là đúng?
A. \(\int\limits_a^b {{m^x}dx} = {m^b} - {m^a}\).
B. \(\int\limits_a^b {{m^x}dx} = {m^a} - {m^b}\).
C. \(\int\limits_a^b {{m^x}dx} = \frac{{{m^b}}}{{\ln m}} - \frac{{{m^a}}}{{\ln m}}\).
D. \(\int\limits_a^b {{m^x}dx} = \frac{{{m^a}}}{{\ln m}} - \frac{{{m^b}}}{{\ln m}}\).
Tính:
a) \(\int\limits_0^1 { - 2dx} \);
b) \(\int\limits_0^1 {\frac{{2x}}{3}dx} \);
c) \(\int\limits_0^1 {{x^4}dx} \);
d) \(\int\limits_1^3 {2\sqrt[3]{x}dx} \);
e) \(\int\limits_1^2 {\frac{2}{{3x}}dx} \);
g) \(\int\limits_1^9 {\left( {x\sqrt x - 2} \right)dx} \).
Tính:
a) \(\int\limits_0^{\frac{\pi }{2}} {\sin xdx} \);
b) \(\int\limits_0^{\frac{\pi }{4}} {\cos xdx} \);
c) \(\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\frac{1}{{{{\sin }^2}x}}dx} \);
d) \(\int\limits_0^{\frac{\pi }{4}} {\frac{1}{{{{\cos }^2}x}}dx} \);
e) \(\int\limits_0^{\frac{\pi }{2}} {\left( {\sin x - 2} \right)dx} \);
g) \(\int\limits_0^{\frac{\pi }{4}} {\left( {3\cos x + 2} \right)dx} \).
Tính:
a) \(\int\limits_0^2 {{e^{ - 5{\rm{x}}}}dx} \);
b) \(\int\limits_0^1 {{3^{x + 2}}dx} \);
c) \(\int\limits_{ - 1}^1 {{3^{2{\rm{x}}}}dx} \).
Tính các tích phân sau:
a) \(\int\limits_0^2 {\left( {3x - 2} \right)\left( {3x + 2} \right)dx} \);
b) \(\int\limits_1^2 {{t^2}\left( {5{t^2} - 2} \right)dt} \);
c) \(\int\limits_{ - 1}^1 {\left( {x - 2} \right)\left( {{x^2} + 2{\rm{x}} + 4} \right)dx} \).
Tính các tích phân sau:
a) \(\int\limits_1^2 {\frac{{1 - 2{\rm{x}}}}{{{x^2}}}dx} \);
b) \(\int\limits_1^2 {{{\left( {\sqrt x + \frac{1}{{\sqrt x }}} \right)}^2}dx} \);
c) \(\int\limits_1^4 {\frac{{x - 4}}{{\sqrt x + 2}}dx} \).
Tính các tích phân sau:
a) \(\int\limits_1^3 {{e^{x - 2}}dx} \);
b) \(\int\limits_0^1 {{{\left( {{2^x} - 1} \right)}^2}dx} \);
c) \(\int\limits_0^1 {\frac{{{e^{2x}} - 1}}{{{e^x} + 1}}dx} \).
Tính các tích phân sau:
a) \(\int\limits_0^\pi {\left( {2\cos x + 1} \right)dx} \);
b) \(\int\limits_0^\pi {\left( {1 + \cot x} \right)\sin xdx} \);
c) \(\int\limits_0^{\frac{\pi }{4}} {{{\tan }^2}xdx} \).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \frac{{\sqrt x - 1}}{x},x > 0\). Tính giá trị của \(f\left( 4 \right) - f\left( 1 \right)\).
Tìm đạo hàm của hàm số \(F\left( x \right) = \sqrt {4x + 1} \). Từ đó, tính tích phân \(\int\limits_0^1 {\frac{1}{{\sqrt {4x + 1} }}dx} \).
Tính:
a) \(\int\limits_1^2 {\frac{{{x^4} + {x^3} + {x^2} + x + 1}}{{{x^2}}}dx} \);
b) \(\int\limits_1^2 {\frac{{x{e^x} + 1}}{x}dx} \);
c) \(\int\limits_0^1 {\frac{{{8^x} + 1}}{{{2^x} + 1}}dx} \);
d) \(\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\frac{{1 + {{\sin }^2}x}}{{1 - {{\cos }^2}x}}dx} \).
Tính
a) \(\int\limits_1^3 {{x^3}dx;} \)
b) \(\int\limits_0^\pi {\cos udu.} \)
a) Cho hàm số \(f(x)\) liên tục trên đoạn \([ - 1;5]\) và \[\int\limits_{ - 1}^5 {\left[ {2x - 3f(x)} \right]} dx = 12\]. Tính \(\int_{ - 1}^5 f (x)dx\).
b) Cho \(f(x) = \left\{ {\begin{array}{*{20}{l}}{{x^3} + 2}&{{\rm{khi }}x > - 1}\\{2x + 3}&{{\rm{khi }}x \le - 1}\end{array}} \right.\). Tính \(\int_{ - 2}^1 f (x)dx\).
