Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a.
-
A.
Tâm là điểm A và bán kính là \(R = a\sqrt 2 \).
-
B.
Tâm là giao điểm hai đường chéo và bán kính là \(R = a\sqrt 2 \).
-
C.
Tâm là giao điểm hai đường chéo và bán kính là \(R = \frac{{a\sqrt 2 }}{2}\).
-
D.
Tâm là điểm B và bán kính là \(R = \frac{{a\sqrt 2 }}{2}\).
Dựa vào tính chất của hình vuông để suy ra tâm đường tròn.
Sử dụng định lí Pythagore để tính bán kính.
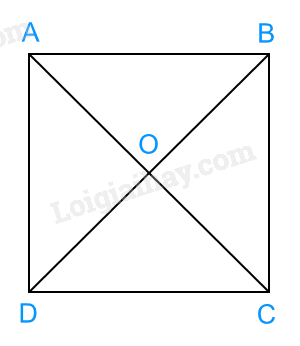
Gọi O là giao điểm của hai đường chéo của hình vuông ABCD.
Khi đó, theo tính chất của hình vuông, ta có: \(OA = OB = OC = OD\) nên O là tâm đường tròn đi qua 4 đỉnh của hình vuông ABCD.
Bán kính của đường tròn là: \(R = OA = \frac{1}{2}AC\).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B, ta có:
\(A{C^2} = A{B^2} + B{C^2} = 2A{B^2} = 2.{a^2}\) suy ra \(AC = \sqrt {2{a^2}} = a\sqrt 2 \)
Do đó \(R = \frac{1}{2}a\sqrt 2 = \frac{{a\sqrt 2 }}{2}\).
Vậy tâm là giao điểm hai đường chéo và bán kính là \(R = \frac{{a\sqrt 2 }}{2}\).
Đáp án C
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
Cho hình chữ nhật $ABCD$ có$AB = 12cm,BC = 5cm$ .Tính bán kính đường tròn đi qua bốn đỉnh $A,B,C,D$.
-
A.
$R = 7,5\,\,cm$
-
B.
$R = 13\,cm$
-
C.
$R = 6cm$
-
D.
$R = 6,5\,cm$
Bài 2 :
Đường tròn tâm $O$ bán kính $5cm$ là tập hợp các điểm:
-
A.
Có khoảng cách đến điểm $O$ nhỏ hơn bằng $5cm$
-
B.
Có khoảng cách đến $O$ bằng $5cm$
-
C.
Cách đều $O$ một khoảng là $5cm$
-
D.
Cả B và C đều đúng.
Bài 3 :
Cho hình chữ nhật \(ABCD\) có \(AB = 8cm,BC = 6cm\) .Tính bán kính đường tròn đi qua bốn đỉnh \(A,B,C,D\).
-
A.
\(R = 5\,\,cm\)
-
B.
\(R = 10\,cm\)
-
C.
\(R = 6cm\)
-
D.
\(R = 2,5\,cm\)
Bài 4 :
Cho tam giác ABC vuông tại A. Chứng minh rằng điểm A thuộc đường tròn đường kính BC.
Bài 5 :
Mở 1 chiếc compa sao cho hai đầu compa cách nhau một khoảng R cho trước. Tì đầu nhọn của compa lên một điểm cố định trên tờ giấy, xoay compa để đầu bút M của compa vạch trên giấy một đường cong. Nêu nhận xét về các khoảng cách từ một điểm M tuỳ ý trên đường cong vừa vẽ đến điểm O.
Bài 6 :
Đồng hồ được mô tả ở Hình 2 có kim phút dài 12cm. Khi kim phút quay một vòng thì đầu mút của kim phút vạch nên đường gì?

Bài 7 :
Hãy chỉ ra một số đồ vật trong thực tiễn gợi nên hình ảnh của đường tròn.
Bài 8 :
Cho tam giác ABC vuông tại A. Tâm đường tròn đi qua ba đỉnh của tam giác ABC là
-
A.
trung điểm của BC.
-
B.
trung điểm của AC.
-
C.
trung điểm của AB.
-
D.
trọng tâm của tam giác ABC.
Bài 9 :
Cho tam giác đều \(ABC\) cạnh bằng \(a\), các đường cao là \(BM\) và \(CN\). Gọi \(D\) là trung điểm của cạnh \(BC\). Đường tròn đi qua bốn điểm \(B\), \(N\), \(M\), \(C\) là
-
A.
đường tròn tâm \(D\) bán kính \(\frac{{BC}}{2}\).
-
B.
đường tròn tâm \(D\) bán kính \(BC\).
-
C.
đường tròn tâm \(B\) bán kính \(\frac{{BC}}{2}\).
-
D.
đường tròn tâm \(C\) bán kính \(\frac{{BC}}{2}\).
Bài 10 :
Cho tam giác ABC cân tại A, đường cao AH = 6cm, BC = 8cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D. Các điểm nào sau đây thuộc cùng một đường tròn?
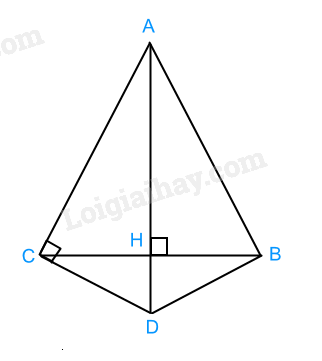
-
A.
D, H, B, C
-
B.
A, B, H, C.
-
C.
A, B, D, H.
-
D.
A, B, D, C.
Bài 11 :
Các bánh xe (xe đạp, ô tô…) đều có dạng hình tròn (với tâm tại trục của bánh xe). Hãy giải thích lí do.
Bài 12 :
Giả định rằng Trái Đất quay xung quanh Mặt Trời theo một quỹ đạo tròn có bán kính khoảng 150 triệu kilômét và phải hết đúng một năm (365 ngày) để hoàn thành một vòng quay. Hãy tính quãng đường Trái Đất đi được trong một ngày (làm tròn đến hàng nghìn theo đơn vị kilômét).
Bài 13 :
Chứng minh bốn đỉnh của hình vuông ABCD có cạnh bằng 16 cm đều nằm trên một đường tròn. Tính bán kính của đường tròn này.
Bài 14 :
Cho tam giác ABC vuông tại A. Tâm đường tròn đi qua ba đỉnh của tam giác ABC là
A. trung điểm của BC.
B. trung điểm của AC.
C. trung điểm của AB.
D. trọng tâm của tam giác ABC.
Bài 15 :
Cho tam giác ABC cân tại A có ba đỉnh nằm trên đường tròn (O). Đường cao AH cắt (O) tại D. Biết \(BC = 24cm,AC = 20cm\). Tính chiều cao AH và bán kính đường tròn (O).


















Danh sách bình luận