Đề bài

Thực hiện phép tính: $\sqrt {\frac{4}{9}:\frac{{25}}{{36}}} $.

A.

$\frac{5}{9}$.
B.

$\frac{2}{3}$.
C.

$\frac{5}{6}$.
D.

$\frac{4}{5}$.

Phương pháp giải

Áp dụng quy tắc khai phương của một thương.

Lời giải của GV Loigiaihay.com

Ta có:

$\sqrt {\frac{4}{9}:\frac{{25}}{{36}}} = \sqrt {\frac{4}{9}} :\sqrt {\frac{{25}}{{36}}} = \frac{2}{3}:\frac{5}{6} = \frac{4}{5}$.

Đáp án D

Đáp án : D

Báo lỗi - Góp ý

BÌNH LUẬN

Danh sách bình luận

Đang tải bình luận...

Các bài tập cùng chuyên đề

Bài 1 :

Kết quả của phép tính $\sqrt {\dfrac{{81}}{{169}}} $ là?

A.

$\dfrac{9}{{13}}$
B.

$\dfrac{9}{{169}}$
C.

$\dfrac{3}{{13}}$
D.

$\dfrac{{13}}{9}$

Xem lời giải >>

Bài 2 :

Kết quả của phép tính $\sqrt {\dfrac{{ - 999}}{{111}}} $ là?

A.

$9$
B.

$-9$
C.

$-3$
D.

Không tồn tại.

Xem lời giải >>

Bài 3 :

Kết quả của phép tính: $\sqrt {\dfrac{{1,21}}{{576}}} $ là?

A.

$\dfrac{{1,1}}{{240}}$
B.

$\dfrac{{11}}{{24}}$
C.

$\dfrac{{11}}{{240}}$
D.

$\dfrac{{240}}{{11}}$

Xem lời giải >>

Bài 4 :

Kết quả của phép tính: $\sqrt {\dfrac{{625}}{{ - 729}}} $ là?

A.

$\dfrac{{25}}{{27}}$
B.

$ - \dfrac{{25}}{{27}}$
C.

$ - \dfrac{5}{7}$
D.

Không tồn tại.

Xem lời giải >>

Bài 5 :

Tính và so sánh: $\sqrt {100} :\sqrt 4 $ và $\sqrt {100:4} .$

Xem lời giải >>

Bài 6 :

Tính:

a) $\sqrt {99} :\sqrt {11} ;$

b) $\sqrt {7,84} ;$

c) $\sqrt {1815} :\sqrt {15} .$

Xem lời giải >>

Bài 7 :

Một vật rơi tự do từ độ cao 396,9 m. Biết quãng đường chuyển động S (mét) của vật phụ thuộc vào thời gian t (giây) bởi công thức $S = 4,9{t^2}.$ Vật chạm đất sau

A. 8 giây.

B. 5 giây.

C. 11 giây.

D. 9 giây.

Xem lời giải >>

Bài 8 :

a) Thực hiện các phép tính có trên bảng trong Hình 2.

b) Từ đó, có nhận xét gì về căn bậc hai của thương hai số dương?

Xem lời giải >>

Bài 9 :

Tính

a) $\sqrt {\frac{9}{{25}}} $

b) $\sqrt {1\frac{9}{{16}}} $

c) $\sqrt {150} :\sqrt 6 $

d) $\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}} $

Xem lời giải >>

Bài 10 :

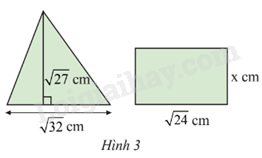
Biết rằng hình tam giác và hình chữ nhật ở Hình 3 có diện tích bằng nhau. Tính chiều rộng x của hình chữ nhật.

Xem lời giải >>

Bài 11 :

Tính

a) $\sqrt {\frac{{0,49}}{{81}}} $

b) $\sqrt {2\frac{7}{9}} $

c) $\sqrt {\frac{1}{{16}}.\frac{9}{{36}}} $

d) $\left( { - \sqrt {52} } \right):\sqrt {13} $

Xem lời giải >>

Bài 12 :

So sánh $\sqrt {\frac{{16}}{{25}}} $ và $\frac{{\sqrt {16} }}{{\sqrt {25} }}$.

Xem lời giải >>

Bài 13 :

Trong tình huống nêu ra ở phần mở đầu, viết hệ số phục hồi của quả bóng rổ dưới dạng phân số.

Xem lời giải >>

Bài 14 :

Áp dụng quy tắc về căn bậc hai của một thương, hãy tính:

a. $\sqrt {\frac{{49}}{{36}}} $

b. $\sqrt {\frac{{{{13}^2} - {{12}^2}}}{{81}}} $

c. $\frac{{\sqrt {{9^3} + {7^3}} }}{{\sqrt {{9^2} - 9.7 + {7^2}} }}$

d. $\frac{{\sqrt {{{50}^3} - 1} }}{{\sqrt {{{50}^2} + 51} }}$

Xem lời giải >>

Bài 15 :

Trong Vật lí, ta có định luật Joule – Lenz để tính nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua: $Q = {I^2}Rt$.

Trong đó: Q là nhiệt lượng tỏa ra trên dây dẫn tính theo Jun (J);

I là cường độ dòng điện chạy trong dây dẫn tính theo Ampe (A);

R là điện trở dây dẫn tính theo Ohm $\left( \Omega \right)$;

t là thời gian dòng điện chạy qua dây dẫn tính theo giây.

Áp dụng công thức trên để giải bài toán sau: Một bếp điện khi hoạt động bình thường có điện trở $R = 80\Omega $. Tính cường độ dòng điện chạy trong dây dẫn, biết nhiệt lượng mà dây dẫn tỏa ra trong 1 giây là 500J.

Xem lời giải >>

Bài 16 :

a) $\sqrt {\frac{9}{{25}}:\frac{{64}}{{121}}} $;

b) $\sqrt {\frac{{81}}{{10}}}:\sqrt {4\frac{9}{{10}}} $.

Xem lời giải >>

Bài 17 :

Tính và so sánh

a) $\sqrt {\frac{9}{{16}}} $ và $\frac{{\sqrt 9 }}{{\sqrt {16} }}$;

b) $\sqrt {\frac{{25}}{4}} $ và $\frac{{\sqrt {25} }}{{\sqrt 4 }}$;

Xem lời giải >>

Bài 18 :

Thực hiện phép tính: $\sqrt {\frac{{{{149}^2} - {{76}^2}}}{{{{457}^2} - {{384}^2}}}} $.

A.

$\frac{7}{{24}}$.
B.

$\frac{2}{{17}}$.
C.

$\frac{{15}}{{29}}$.
D.

$\frac{{16}}{{49}}$.

Xem lời giải >>

Bài 19 :

Tính

a) $\sqrt {\frac{{16}}{{121}}} $

b) $\sqrt {4\frac{{21}}{{25}}} $

c) $\sqrt {\frac{{6,4}}{{8,1}}} $

d) $\frac{{\sqrt {300} }}{{\sqrt {27} }}$

e) $\frac{{\sqrt 6 }}{{\sqrt {150} }}$

g) $\sqrt {\frac{3}{2}} :\sqrt {\frac{1}{{24}}} $

Xem lời giải >>

Bài 20 :

Áp dụng quy tắc về căn bậc hai của một thương, hãy tính:

a) $\sqrt {\frac{{1,21}}{{0,49}}} $

b) $\frac{{\sqrt {15} }}{{\sqrt {735} }}$

c) $\frac{{\sqrt {12,5} }}{{\sqrt {0,5} }}$

d) $\frac{{\sqrt 8 }}{{\sqrt {{4^4}{{.2}^3}} }}$

Xem lời giải >>

Bài 21 :

Tính

a) $\sqrt {99} :\sqrt {11} $;

b) $\sqrt {7,84} $;

c) $\sqrt {1815} :\sqrt {15} $.

Xem lời giải >>

Bài 22 :

Vận tốc (m/s) của một vật đang bay được cho bởi công thức $v = \sqrt {\frac{{2E}}{m}} $, trong đó E là động năng của vật (tính bằng Joule, kí hiệu là J) và m (kg) là khối lượng của vật (Theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).

Tính vận tốc bay của một vật khi biết vật đó có khối lượng 2,5kg và động năng 281,25J.

Xem lời giải >>

Thực hiện phép tính: \(\sqrt {\frac{4}{9}:\frac{{25}}{{36}}} \).