Số lượng sản phẩm bán được cho một công ty trong x (tháng) được tính theo công thức
\(S\left( x \right) = 200\left( {5 - \frac{9}{{2 + x}}} \right)\) trong đó \(x \ge 1\).
a) Xem \(y = S\left( x \right)\) là một hàm số xác định trên nửa khoảng \([1; + \infty )\), hãy tìm tiệm cận ngang của đồ thị hàm số đó.
b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn.
a) Đường thẳng \(y = {y_o}\) được gọi là đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_o}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_o}\).
b) Dựa vào câu a) để kết luận
a) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } S\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } S\left( x \right) = 1000\).
Vậy đường thẳng \(y = 1000\) là đường tiệm cận ngang của đồ thị hàm số \(S\left( x \right)\).
b) Khi x đủ lớn thì số lượng sản phẩm bán được của công ti đó trong tháng x sẽ gần đạt được 1000 sản phẩm.

Các bài tập cùng chuyên đề
Bài 1 :
Số tiệm cận ngang của đồ thị hàm số \(y = 2x - 1 + \sqrt {4{x^2} - 4} \) là
-
A.
\(2\)
-
B.
\(1\)
-
C.
\(0\)
-
D.
\(3\)
Bài 2 :
Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{{\sqrt {5 + x} - 1}}{{{x^2} + 4x}}.$
-
A.
Đồ thị hàm số không có tiệm cận đứng
-
B.
$x = - {\mkern 1mu} 4.$
-
C.
$x = 0.$
-
D.
$x = 0;{\mkern 1mu} {\mkern 1mu} x = - {\mkern 1mu} 4.$
Bài 3 :
Cho hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{x}\) có đồ thị (C). Với \(x > 0\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = 2\) (H.1.19).
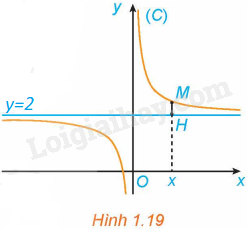
a) Tính khoảng cách MH.
b) Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
Bài 4 :
Tìm tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\).
Bài 5 :
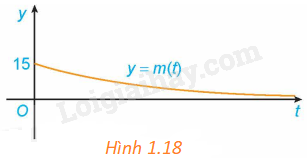
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số \(m\left( t \right) = 15{e^{ - 0,012t}}\). Khối lượng m(t) thay đổi ra sao khi \(t \to + \infty \)? Điều này thể hiện trên Hình 1.18 như thế nào?
Bài 6 :
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là \(C\left( x \right) = 2x + 50\) (triệu đồng). Khi đó, \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Tính chất này nói lên điều gì?
Bài 7 :
Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là \(C\left( x \right) = 2x + 45\) (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\). Hãy giải thích tại sao chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/ sản phẩm. Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình 1.27 như thế nào?

Bài 8 :
Tìm tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x - 2}}{{x + 1}}\).
Bài 9 :
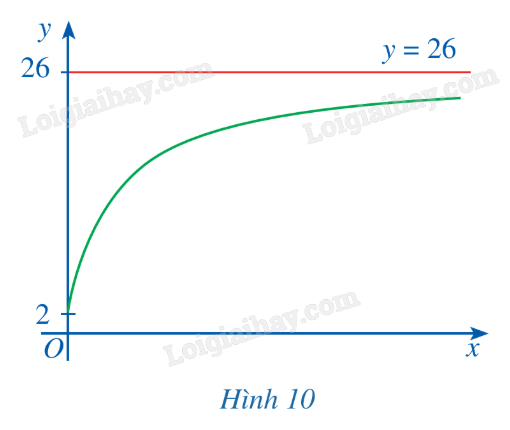
Xét hàm số \(y = f\left( x \right) = \frac{{26x + 10}}{{x + 5}}\) với \(x \in [0; + \infty )\) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).

Bài 10 :
Đồ thị hàm số ở Hình 18a, Hình 18b đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau đây?

a) \(y = \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}}\).
b) \(y = \frac{{2{x^2} + x + 1}}{{x - 1}}\)
c) \(y = \frac{{2{x^2} - 2}}{{{x^2} + 2}}\)
Bài 11 :
Tìm tiệm cận ngang của đồ thị các hàm số sau:
a) \(f(x) = \frac{{x - 1}}{{4x + 1}}\)
b) \(g(x) = \frac{{\sqrt x }}{{\sqrt x + 2}}\)
Bài 12 :
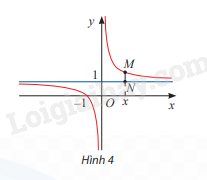
Cho hàm số \(y = \frac{{x + 1}}{x}\) có đồ thị như Hình 4.
a) Tìm \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x},\mathop {\lim }\limits_{x \to - \infty } = \frac{{x + 1}}{x}\)
b) Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = 1 tại điểm N (Hình 4). Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to - \infty \)
Bài 13 :
Nồng độ oxygen trong hồ theo thời gian \(t\) cho bởi công thức \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\), với \(y\) được tính theo \(mg/l\) và \(t\) được tính theo giờ, \(t \ge 0\). Tìm các đường tiệm cận của đồ thị hàm số \(y(t)\). Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian \(t\) trở nên rất lớn?
(Theo: www.researchgate.net/publication/264903978_Microrespirometric_ characterization_of_activated_sludge_inhibition_by_copper_and_zinc)
Bài 14 :
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
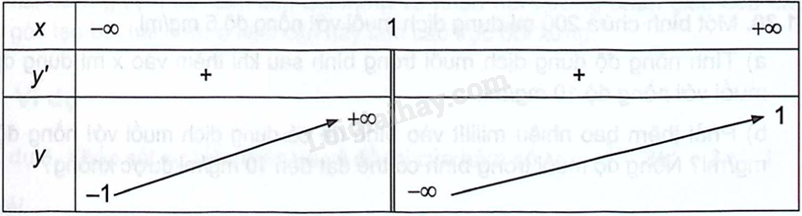
Tìm tiệm cận ngang của đồ thị hàm số \(y = g(x) = \frac{1}{{2 + f(x)}}\).
Bài 15 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{5{\rm{x}} - 2}}{{x + 3}}\) là đường thẳng:
A. \(x = - 3\).
B. \(x = 5\).
C. \(y = - 3\).
D. \(y = 5\).
Bài 16 :
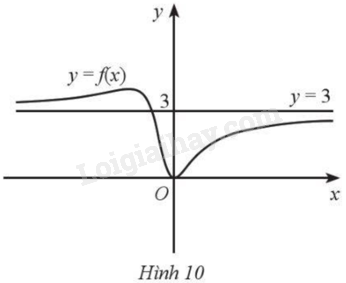
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và đồ thị có đường tiệm cận ngang như Hình 10. Hàm số \(y = f\left( x \right)\) có thể là hàm số nào trong các hàm số sau?
A. \(f\left( x \right) = \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}}\).
B. \(f\left( x \right) = \frac{{2{{\rm{x}}^2}}}{{{x^2} + x + 1}}\).
C. \(f\left( x \right) = \frac{{{{\rm{x}}^2}}}{{{x^2} + x + 1}}\).
D. \(f\left( x \right) = \frac{{{{\rm{x}}^2}}}{{3{x^2} + x + 1}}\).
Bài 17 :
Đồ thị hàm số nào sau đây nhận đường thẳng \(y = - 2\) làm tiệm cận ngang?
A. \(y = \frac{{2{\rm{x}} - 1}}{{ - 1 + x}}\).
B. \(y = \frac{{ - x + 1}}{{2{\rm{x}} - 1}}\).
C. \(y = \frac{{x + 1}}{{x + 2}}\).
D. \(y = \frac{{ - 2{\rm{x + }}1}}{{x - 3}}\).
Bài 18 :
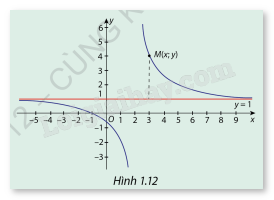
Cho hàm số \(y = f(x) = \frac{{x + 1}}{{x + 2}}\) có đồ thị (C) là đường cong (Hình 1.12). Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)M(x;y) tới đường thẳng y = 1 khi \(x \to + \infty \) và \(x \to - \infty \).
Bài 19 :
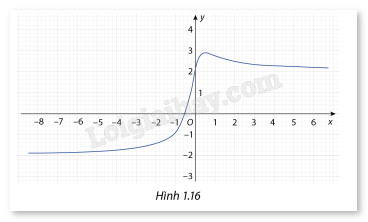
Cho hàm số \(y = f(x) = \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\) có đồ thị như Hình 1.16
a) Tìm các đường tiệm cận ngang của đô thị nếu có.
b) Vẽ các đường tiệm cận ngang vừa tìm được nếu có.
Bài 20 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x + 3}}{{5x + 1}}\) là
-
A.
\(y = 5\)
-
B.
\(y = \frac{1}{5}\)
-
C.
\(y = - \frac{1}{5}\)
-
D.
\(y = 3\)
Bài 21 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x - 3}}{{2 - x}}\) là
-
A.
\(y = 3\)
-
B.
\(y = \frac{1}{2}\)
-
C.
\(y = - 1\)
-
D.
\(y = 2\)
Bài 22 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{ - 1}}{{2 + x}}\) là
-
A.
\(y = - 1\)
-
B.
\(y = - 2\)
-
C.
\(y = - \frac{1}{2}\)
-
D.
\(y = 0\)
Bài 23 :
Trong Vật lý, ta biết rằng khi mắc song song hai điện trở \({R_1}\) và \({R_2}\), thì điện trở tương đương R của mạch điện được tính theo công thức \(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) (theo Vật lý đại cương, NXB Giáo dục Việt Nam, 2016). Giả sử một điện trở \(10\Omega \) được mắc song song với một biến trở x thì điện trở tương đường R là hàm số \(\)\(y = \frac{{10x}}{{10 + x}}\) với x > 0. Điện trở tương đương của mạch không thể vượt quá bao nhiêu?
Bài 24 :
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) \(\left( {c \ne 0;ad - bc \ne 0} \right)\) có đồ thị như hình vẽ bên. Tiệm cận ngang của đồ thị hàm số là:

-
A.
\(x = - 1\)
-
B.
\(y = \frac{1}{2}\)
-
C.
\(y = - 1\)
-
D.
\(x = \frac{1}{2}\)
Bài 25 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{4x + 1}}{{x - 1}}\) là
-
A.
\(y = \frac{1}{4}\)
-
B.
\(y = 4\)
-
C.
\(y = 1\)
-
D.
\(y = - 1\)
Bài 26 :
Cho hàm số f(x) liên tục trên mỗi khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { - \frac{1}{2}; + \infty } \right)\), có bảng biến thiên như hình vẽ:
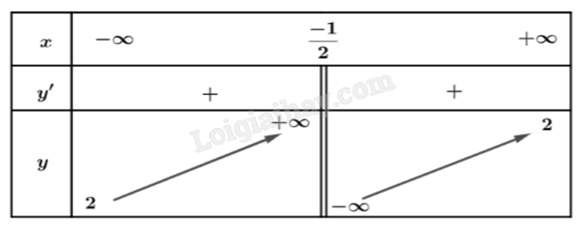
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình
-
A.
\(y = - \frac{1}{2}\)
-
B.
\(x = 2\)
-
C.
\(y = 2\)
-
D.
\(x = - \frac{1}{2}\)
Bài 27 :
Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x - 2024}}{{x + 1}}\) là
-
A.
\(y = - 1\)
-
B.
\(x = 2\)
-
C.
\(y = \frac{1}{2}\)
-
D.
\(y = 2\)
Bài 28 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{4x + 1}}{{x - 1}}\) là
-
A.
\(y = \frac{1}{4}\)
-
B.
\(y = 4\)
-
C.
\(y = 1\)
-
D.
\(y = - 1\)
Bài 29 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 4}}{{x - 1}}\) là đường thẳng
-
A.
x = 2
-
B.
x = 1
-
C.
y = 2
-
D.
y = 1
Bài 30 :
Số dân của một thị trấn sau x năm kể từ năm 1970 được ước tính bởi công thức
\(y = f(x) = \frac{{26x + 10}}{{x + 5}}\)
(f(x) được tính bằng nghìn người) (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020). Xem y = f(x) là một hàm số xác định trên nửa khoảng \([0; + \infty )\), đồ thị của hàm số đó là đường cong màu xanh ở Hình 10.
Khi \(x \to + \infty \), đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng nào?


















Danh sách bình luận