Tính diện tích hình phẳng giới hạn bởi các đường \(y = {x^2} - 1;y = x + 5,x = - 2,x = 3\).
Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
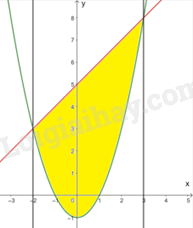
Diện tích hình cần tính là: \(S = \int\limits_{ - 2}^3 {\left| {\left( {x + 5} \right) - \left( {{x^2} - 1} \right)} \right|dx} = \int\limits_{ - 2}^3 {\left( { - {x^2} + x + 6} \right)dx} \)
\( = \left( {\frac{{ - {x^3}}}{3} + \frac{{{x^2}}}{2} + 6x} \right)\left| \begin{array}{l}3\\ - 2\end{array} \right. = \frac{{27}}{2} + \frac{{22}}{3} = \frac{{125}}{6}\)

Các bài tập cùng chuyên đề
Bài 1 :
Tính diện tích hình phẳng giới hạn bởi parabol \(y = {x^2} - 4\), trục hoành và hai đường thẳng \(x = 0,x = 3\) (H.4.15).
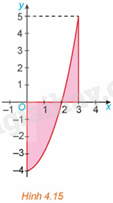
Bài 2 :
Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau \(\left( {{x_o};{p_o}} \right)\) của đồ thị hàm cầu \(p = D\left( x \right)\) và đồ thị hàm cung \(p = S\left( x \right)\) được gọi là điểm cân bằng.
Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang \(p = {p_o}\) và đường thẳng đứng \(x = 0\) là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang \(p = {p_o}\) và đường thẳng đứng \(x = 0\) được gọi là thặng dư sản xuất, như trong Hình 4.19.
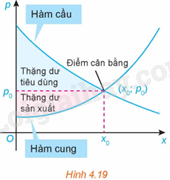
(Theo R. Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009)
Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:
Hàm cầu: \(p = - 0,36x + 9\) và hàm cung: \(p = 0,14x + 2\), trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.
Bài 3 :
Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = \sqrt x ,y = x - 2\) và hai đường thẳng \(x = 1,x = 4\).
Bài 4 :
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(f\left( x \right) = - {x^2} + 4x,\) \(g\left( x \right) = x\) và hai đường thẳng \(x = 1,x = 3\) (H.4.16)
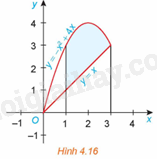
a) Giả sử \({S_1}\) là diện tích hình phẳng giới hạn bởi parabol \(y = - {x^2} + 4x\), trục hoành và hai đường thẳng \(x = 1,x = 3\); \({S_2}\) là diện tích hình phẳng giới hạn bởi đường thẳng \(y = x\), trục hoành và hai đường thẳng \(x = 1,x = 3\). Tính \({S_1}\), \({S_2}\) và từ đó suy ra S.
b) Tính \(\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) và so sánh với S.
Bài 5 :
Xét hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right) = x + 1\), trục hoành và hai đường thẳng \(x = - 2,x = 1\) (H.4.12).
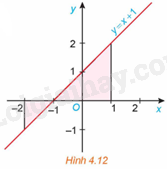
a) Tính diện tích S của hình phẳng này.
b) Tính \(\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx} \) và so sánh với S.
Bài 6 :
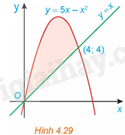
Tính diện tích của hình phẳng được tô màu trong Hình 4.29.
Bài 7 :
Tính diện tích của hình phẳng giới hạn bởi các đường:
a) \(y = {e^x},y = {x^2} - 1,x = - 1,x = 1\);
b) \(y = \sin x,y = x,x = \frac{\pi }{2},x = \pi \);
c) \(y = 9 - {x^2},y = 2{x^2},x = - \sqrt 3 ,x = \sqrt 3 \);
d) \(y = \sqrt x ,y = {x^2},x = 0,x = 1\).
Bài 8 :
Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi x là đại diện cho phần trăm số gia đình trong một quốc gia và y là phần trăm tổng thu nhập, mô hình \(y = x\) sẽ đại diện cho một quốc gia mà các gia đình có thu nhập như nhau. Đường cong Lorenz \(y = f\left( x \right)\), biểu thị phân phối thu nhập thực tế. Diện tích giữa hai mô hình này, với \(0 \le x \le 100\), biểu thị “sự bất bình đẳng về thu nhập” của một quốc gia. Năm 2005, đường cong Lorenz của Hoa Kỳ có thể được mô hình hóa bởi hàm số \(y = {\left( {0,00061{x^2} + 0,0218x + 1\;723} \right)^2},0 \le x \le 100\), trong đó x được tính từ các gia đình nghèo nhất đến giàu có nhất (Theo R. Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009). Tìm sự bất bình đẳng thu nhập của Hoa Kỳ vào năm 2005.
Bài 9 :
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 2x,y = - {x^2} + 4x\) và hai đường thẳng \(x = 0,x = 3\) là
A. \( - 9\).
B. 9.
C. \(\frac{{16}}{3}\).
D. \(\frac{{20}}{3}\).
Bài 10 :
Cho đồ thị hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\) như Hình 4.32.
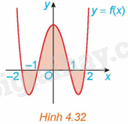
Biết \(\int\limits_{ - 2}^{ - 1} {f\left( x \right)dx} = \int\limits_1^2 {f\left( x \right)dx} = \frac{{ - 22}}{{15}}\) và \(\int\limits_{ - 1}^1 {f\left( x \right)dx} = \frac{{76}}{{15}}\). Khi đó, diện tích của hình phẳng được tô màu là
A. 8.
B. \(\frac{{22}}{{15}}\).
C. \(\frac{{32}}{{15}}\).
D. \(\frac{{76}}{{15}}\).
Bài 11 :
Tính diện tích hình phẳng giới hạn bởi các đường \(y = {e^x},y = x,x = 0\) và \(x = 1\).
Bài 12 :
Cho hàm số f(x) liên tục trên \(\mathbb{R}\). Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 1\) và \(x = 4\) như hình bên.
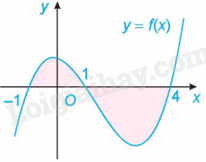
Khẳng định nào dưới đây là đúng?
A. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
B. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
C. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
D. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
Bài 13 :
Cho các hàm số \(y = {2^x}\), y = x
Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số \(y = {2^x}\)
Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số y = x
Gọi S là phẳng giới hạn bởi các đồ thị hàm số \(y = {2^x}\), y = x và hai đường thẳng x = 1, x = 2
(Hình 14)
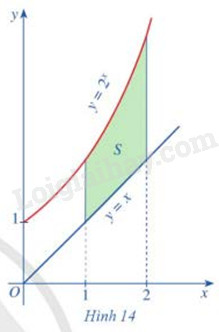
a) Biểu diễn S theo \({S_1},{S_2}\)
b) So sánh S và \(\int\limits_1^2 {({2^x} - x)dx} \)
Bài 14 :
Cho hàm số \(y = f(x) = {x^3} - 2{x^2} - x + 2\) có đồ thị minh họa ở Hình 11.

a) Quan sát Hình 11, hãy cho biết các hình phẳng \({H_1},{H_2},{H_3}\) lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào
b) Tính diện tích \({S_{{H_1}}},{S_{{H_2}}},{S_{{H_3}}}\) của các hình phẳng đó
c) Gọi H là tập hợp của các hình phẳng \({H_1},{H_2},{H_3}\). Hình phẳng H được gọi là hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng x = 0, x = 3. Chứng tỏ rằng diện tích \({S_H}\) của hình phẳng H bằng \({S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^3 {\left| {f(x)} \right|dx} \)
Bài 15 :
Hình thang cong ABCD ở Hình 28 có diện tích bằng:
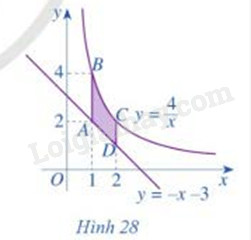
A. \(\int\limits_1^2 {\left( {\frac{4}{x} - x + 3} \right)dx} \)
B. \(\int\limits_1^2 {\left( {\frac{4}{x} + x + 3} \right)dx} \)
C. \(\int\limits_1^2 {\left( {\frac{4}{x} - x - 3} \right)dx} \)
D. \(\int\limits_2^4 {\left( {\frac{4}{x} + x + 3} \right)dx} \)
Bài 16 :
Cho đồ thị hàm số \(y = {e^x}\) và hình phẳng được tô màu như Hình 29
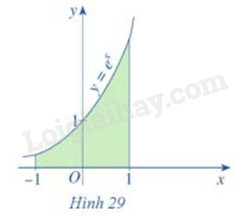
a) Hình phẳng đó được giới hạn bởi các đường nào?
b) Tính diện tích hình phẳng đó
Bài 17 :
Cho đồ thị các hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\), y = x + 1 và hình phẳng được tô màu như hình 30
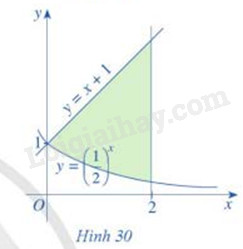
a) Hình phẳng đó được giới hạn bởi các đường nào?
b) Tính diện tích hình phẳng đó
Bài 18 :
Cho đồ thị hàm số y = f(t) như hình 32
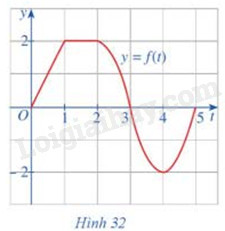
a) Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f(t), trục Ot và hai đường thẳng t = 0, t = 2
b) Hỏi \(\int\limits_0^1 {f(u)du} \) biểu thị cho phần diện tích của hình phẳng giới hạn bởi các đường nào trong Hình 32?
Bài 19 :
Người ta dự định lắp kính cho cửa của một mái vòm có dạng hình parabol. Hãy tính diện tích mặt kính cần lắp vào, biết rằng vòm cửa cao 21m và rộng 70m (Hình 33)

Bài 20 :
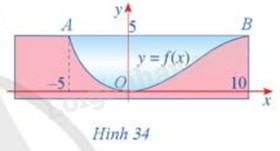
Hình 34 minh họa mặt cắt đứng của một con kênh đặt trong hệ trục tọa độ Oxy. Đáy của con kênh là một đường cong cho bởi phương trình \(y = f(x) = \frac{3}{{100}}\left( { - \frac{1}{3}{x^3} + 5{x^2}} \right)\). Hãy tính diện tích hình phẳng tô màu xanh trong Hình 34, biết đơn vị trên mỗi trục tọa độ là mét
Bài 21 :
Giả sử A, B lần lượt là diện tích các hình được tô màu ở Hình 37
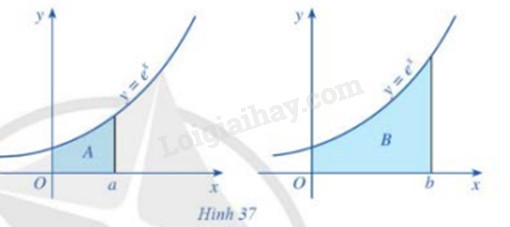
a) Tính các diện tích A, B
b) Biết B = 3A. Biểu diễn b theo a
Bài 22 :
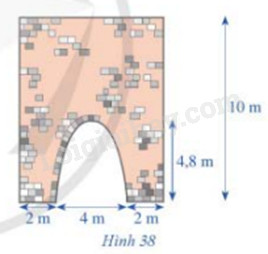
Hình 38 minh họa mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với một cổng ra vào có dạng hình parabol với các kích thước được cho như trong hình đó. Người ta dự định sơn lại mặt ngoài của bức tường đó. Chi phí để sơn lại bức tường là 15 000 đồng/ 1\({m^2}\). Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó sẽ là bao nhiêu
Bài 23 :
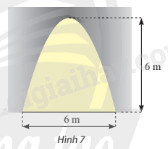
Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 7. Tính diện tích của cửa hầm.
Bài 24 :
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = 5x - {x^2}\), \(y = {x^2} - x\) và hai đường thẳng \(x = 0\), \(x = 2\).
Bài 25 :
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2} - 2x - 1\), \(y = x - 1\) và hai đường thẳng \(x = 1\), \(x = 4\).
Bài 26 :
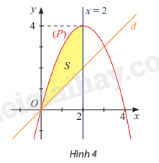
Cho hai hàm số \(y = 4x - {x^2}\) và \(y = x\) lần lượt có đồ thị \(\left( P \right)\) và \(d\) như hình 4.
a) Tính diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\).
b) Tính diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\).
Bài 27 :
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \cos x - 2\), trục hoành và hai đường thẳng \(x = 0\), \(x = \pi \).
Bài 28 :
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2x - {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 3\).
Bài 29 :
Gọi \(d\) là đồ thị của hàm số \(y = f\left( x \right) = 6 - 2x\). Kí hiệu \({S_1}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và trục tung; \({S_2}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và đường thẳng \(x = 5\) (Hình 1).
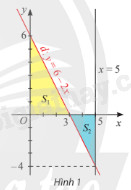
a) Tính \({S_1}\) và so sánh với \(\int\limits_0^3 {f\left( x \right)dx} \).
b) Tính \({S_2}\) và so sánh với \(\int\limits_3^5 {f\left( x \right)dx} \).
c) So sánh \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} \) với \({S_1} + {S_2}\).
Bài 30 :
Tính diện tích hình phẳng giới hạn bởi
a) Đồ thị của hàm số \(y = {e^x}\), trục hoành và hai đường thẳng \(x = - 1\), \(x = 1\).
b) Đồ thị của hàm số \(y = x + \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\).


















Danh sách bình luận