Trên mặt phẳng tọa độ Oxy, vẽ hai đường thẳng \(x + y = 4\) và \(2x - y = 5\). Tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}x + y = 4\\2x - y = 5\end{array} \right.\).
-
A.
\(\left( {4;4} \right)\).
-
B.
\(\left( {\frac{5}{2}; - 5} \right)\).
-
C.
\(\left( {3;1} \right)\).
-
D.
\(\left( {1;3} \right)\).
Vẽ hai đường thẳng \(x + y = 4\) và \(2x - y = 5\) trên mặt phẳng tọa độ.
Tìm giao điểm của hai đường thẳng đó.
Ta có:
\(\begin{array}{l}\left( {{d_1}} \right):x + y = 4\\y = - x + 4\end{array}\)
Cho x = 0 suy ra y = 4
Cho y = 0 suy ra x = 4
Đường thẳng \(x + y = 4\) là đường thẳng đi qua hai điểm \(\left( {0;4} \right),\left( {4;0} \right)\).
\(\begin{array}{l}\left( {{d_2}} \right):2x - y = 5\\y = 2x - 5\end{array}\)
Cho x = 0 suy ra y = -5.
Cho y = 0 suy ra x = \(\frac{5}{2}\).
Đường thẳng \(2x - y = 5\) là đường thẳng đi qua hai điểm \(\left( {0; - 5} \right),\left( {\frac{5}{2};0} \right)\).
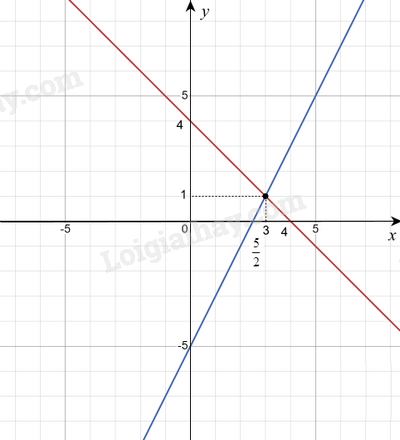
Nhìn vào đồ thị ta thấy \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại điểm có tọa độ \(\left( {3;1} \right)\).
Đáp án C
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
a) Hệ phương trình \(\left\{ \begin{array}{l}2x = - 6\\5x + 4y = 1\end{array} \right.\) có là một hệ hai phương trình bậc nhất hai ẩn không, vì sao?
b) Cặp số \(\left( { - 3;4} \right)\) có là một nghiệm của hệ phương trình đó hay không, vì sao?
Bài 2 :
Cho các cặp số \(\left( { - 2;1} \right),\left( {0;2} \right),\left( {1;0} \right),\left( {1,5;3} \right),\left( {4; - 3} \right)\) và hai phương trình
\(\begin{array}{l}5x + 4y = 8,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\3x + 5y = - 3.\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)
Trong các cặp số đã cho:
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ hai phương trình gồm (1) và (2)?
c) Vẽ hai đường thẳng \(5x + 4y = 8\) và \(3x + 5y = - 3\) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Bài 3 :
Cho hai đường thẳng \(y = - \frac{1}{2}x + 2\) và y = -2x – 1.
a) Vẽ hai đường thẳng đó trên cùng mặt phẳng toạ độ Oxy.
b) Xác định toạ độ giao điểm A của hai đường thẳng trên.
c) Toạ độ của điểm A có là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 2y = 4}\\{2x + y = - 1}\end{array}} \right.\) không? Tại sao?
Bài 4 :
Giải các hệ phương trình:
a) \(\left\{ {\begin{array}{*{20}{c}}{3x + 2y = 7}\\{x - 7y = - 13}\end{array}} \right.\)
b) \(\left\{ {\begin{array}{*{20}{c}}{4x + y = 2}\\{8x + 3y = 5}\end{array}} \right.\)
c) \(\left\{ {\begin{array}{*{20}{c}}{5x - 4y = 3}\\{2x + y = 4}\end{array}} \right.\)
d) \(\left\{ {\begin{array}{*{20}{c}}{3x - 2y = 10}\\{x - \frac{2}{3}y = 3\frac{1}{3}}\end{array}} \right.\)
Bài 5 :
Hai bạn Dũng, Huy vào siêu thị mua vở và bút bi để ủng hộ các bạn học sinh vùng lũ lụt. Bạn Dũng mua 5 quyển vở và 3 chiếc bút bi với tổng số tiền phải trả là 39 000 đồng. Bạn Huy mua 6 quyển vở và 2 chiếc bút bi với tổng số tiền phải trả là 42 000 đồng. Giả sử giá của mỗi quyển vở là \(x\) đồng \(\left( {x > 0} \right)\), giá của mỗi chiếc bút bi là \(y\) đồng \(\left( {y > 0} \right)\).
a. Viết hai phương trình bậc nhất hai ẩn \(x,y\) lần lượt biểu thị tổng số tiền phải trả của bạn Dũng, bạn Huy.
b. Cặp số \(\left( {x;y} \right) = \left( {6\,\,000;3\,\,000} \right)\) có phải là nghiệm của từng phương trình bậc nhất đó hay không? Vì sao?
Bài 6 :
Nhân dịp tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh: bánh nướng và bánh dẻo. Lượng đường cần cho mỗi chiếc bánh nướng, bánh dẻo lần lượt là 60g, 50g. Gọi \(x\) và \(y\) lần lượt là số lượng bánh nướng, bánh dẻo mà doanh nghiệp dự định sản xuất để lượng đường sản xuất bánh là 500kg. Viết phương trình bậc nhất hai ẩn \(x,y\) và chỉ ra ba nghiệm của phương trình đó.

Bài 7 :
Năm bạn Châu, Hà, Khang, Minh, Phong cùng đi mua sticker để trang trí vở. Có hai loại sticker: loại I giá 2 nghìn đồng/chiếc và loại II giá 3 nghìn đồng/chiếc. Mỗi bạn mua 1 chiếc và tổng số tiền năm bạn phải trả là 12 nghìn dồng. Gọi \(x\) và \(y\) lần lượt là số sticker loại I và loại II mà năm bạn đã mua.
a. Viết hệ phương trình bậc nhất hai ẩn \(x;y\).
b. Cặp số \(\left( {3;2} \right)\) có phải là nghiệm của hệ phương trình câu a hay không? Vì sao?
Bài 8 :
Để chuẩn bị cho buổi liên hoan của gia đình, bác Ngọc mua hai loại thực phẩm là thịt lợn và cá chép. Giá tiền thịt lợn là 130 nghìn đồng/kg, giá tiền cá chép là 50 nghìn đồng/kg. Bác Ngọc đã chi 295 nghìn đồng để mua 3,5kg hai loại thực phẩm trên. Gọi \(x\) và \(y\) lần lượt là số kilôgam thịt lợn và cá chép mà bác Ngọc đã mua.
a. Viết hệ phương trình bậc nhất hai ẩn \(x,y\).
b. Cặp số \(\left( {1,5;2} \right)\) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Bài 9 :
Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 1 (đơn vị: kg/1 sản phẩm).
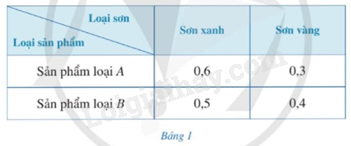
Người ta dự định sử dụng 85kg sơn xanh và 50kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Gọi \(x;y\) lần lượt là số sản phẩm loại A, số sản phẩm loại B được sơn.
a. Viết hệ phương trình bậc nhất hai ẩn x, y.
b. Cặp số \(\left( {100;50} \right)\) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Bài 10 :
Giải các hệ phương trình:
a. \(\left\{ \begin{array}{l}x + 3y = - 2\\5x + 8y = 11\end{array} \right.\)
b. \(\left\{ \begin{array}{l}2x + 3y = - 2\\3x - 2y = - 3\end{array} \right.\)
c. \(\left\{ \begin{array}{l}2x - 4y = - 1\\ - 3x + 6y = 2\end{array} \right.\)
Bài 11 :
Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}2\left( {x + y} \right) + 3\left( {x - y} \right) = 4\\\left( {x + y} \right) + 2\left( {x - y} \right) = 5\end{array} \right.\)
b) \(\left\{ \begin{array}{l}3\left( {x + 2y} \right) - 4\left( {2x - y} \right) = 5\\4\left( {x + 2y} \right) + 3\left( {2x - y} \right) = 15\end{array} \right.\)
Bài 12 :
Khám phá thêm các bài toán dân gian bằng thơ gắn với hệ hai phương trình bậc nhất hai ẩn.
Bài 13 :
Cho hệ phương trình \(\left\{ \begin{array}{l}2x = - 6\\5x + 4y = 1\end{array} \right.\)
a) Hệ phương trình trên có là một hệ phương trình bậc nhất hai ẩn không? Vì sao?
b) Cặp số \(\left( { - 3;4} \right)\) có là một nghiệm của hệ phương trình đã cho hay không? Vì sao?
Bài 14 :
Cho các cặp số (-2; 1), (0; 2), (1; 0), (1,5; 3), (4; -3) và hai phương trình
\(5x + 4y = 8\), (1)
\(3x + 5y = - 3\) (2)
Trong các cặp số đã cho:
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?
c) Vẽ hai đường thẳng \(5x + 4y = 8\) và \(3x + 5y = - 3\) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Bài 15 :
Cho ba phương trình x + 2y = -1; 2x – y = 7; - x + 3y = -9
Hãy lập một hệ hai phương trình bậc nhất hai ẩn từ ba phương trình đã cho sao cho hệ cặp số (3; - 2) làm nghiệm.
Bài 16 :
Cho hai đường thẳng \(y = - \frac{1}{2}x - 3\) và y = -3x + 2. Vẽ hai đường thẳng đó trên cùng một hệ trục toạ độ. Xác định toạ độ giao điểm A của hai đường thẳng và cho biết toạ độ của điểm A có là nghệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 2y = - 6}\\{3x + y = 2}\end{array}} \right.\) không. Tại sao?
Bài 17 :
Ba bạn An, Bình, Chi cùng đi nhà sách. Cả ba bạn đã mua hết 279 000 đồng. Ba bạn đã mua 3 quyển truyện với giá 45 000 đồng/quyền và mua thêm bút bi và bút chì màu. Giá của bút bi và bút chì màu lần lượt là 3 600 đồng/chiếc và 5 000 đồng/chiếc. Gọi x và y lần lượt là số chiếc bút bi và bút chì màu mà ba bạn đã mua. Viết phương trình bậc nhất hai ẩn cho số tiền mà ba bạn đã dùng để mua bút bi, bút chì màu và chỉ ra một nghiệm của phương trình đó.
Bài 18 :
Cô Hà sử dụng dịch vụ điện thoại di động với giá cước gọi nội mạng và gọi ngoại mạng lần lượt là 1 190 đồng/phút và 1 390 đồng/phút. Trong tháng 10, cô Hà đã sử dụng 500 phút gọi (cả nội mạng và ngoại mạng) với tiền cước là 635 000 đồng. Gọi x và y lần lượt là số phút gọi nội mạng và ngoại mạng trong tháng 10 của cô Hà.
a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.
b) Cặp số (300 ; 200) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Bài 19 :
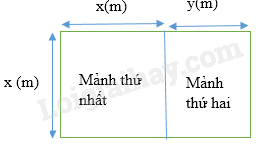
Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh x (m); mảnh đất thứ hai có dạng hình chữ nhật với chiều dài x (m) và chiều rộng y (m) (x > y > 0) được minh hoạ ở Hình 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6.8 m. Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1 130 000 đồng theo giá 50000 đồng một mét.
a) Viết hệ hai phương trình bậc nhất hai ấn x, y biểu thị mối quan hệ giữa các đại lưọng.
b) Cặp số (13 ; 9,6) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Bài 20 :
Người ta muốn pha dung dịch HNO3 30% với dung dịch HNO3 55% để được dung dịch HNO3 50%. Gọi x và y lần lượt là số gam dung dịch HNO3 30% và HNO3 55% cần dùng để pha được 100g dung dịch HNO3 50%.
a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.
b) Cặp số (20 ; 80) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Bài 21 :
Một ô tô đi từ địa điểm A đến địa điểm B với tốc độ x (km/h) thì đi hết y (giờ) với x > 10 và y > 0,5. Nếu tốc độ của ô tô giảm 10 km/h thì thời gian ô tô đã tăng 45 phút. Nếu tốc độ của ô tô tăng 10 km/h thì thời gian ô tô đi giảm 30 phút.
a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.
b) Cặp số (50 ; 3) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Bài 22 :
Cho các cặp số (-2; 2), (1; 1), (4; 1), (8; -2) và hai phương trình:
\(x + 3y = 4\); (1)
\(2x - 5y = - 3\). (2)
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ gồm hai phương trình (1) và phương trình (2)?
c) Vẽ hai đường thẳng \(d:x + 3y = 4\) và \(d':2x - 5y = - 3\) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Bài 23 :
Bằng cách vẽ các đường thẳng thích hợp trên cùng một mặt phẳng tọa độ, hãy tìm nghiệm của mỗi hệ phương trình sau:
a) \(\left\{ \begin{array}{l}2x = - 4\\3x - y = 5\end{array} \right.\);
b) \(\left\{ \begin{array}{l}x - 2y = 4\\2y = - 3\end{array} \right.\).
Bài 24 :
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{2x + 0y = 0}\\{5x + 7y = 14}\end{array}} \right.\).
a) Hệ phương trình đã cho không phải là hệ phương trình bậc nhất hai ẩn.
b) Hệ phương trình đã cho có vô số nghiệm.
c) Hệ phương trình đã cho vô nghiệm.
d) Hệ phương trình đã cho có nghiệm duy nhất là (0;2).


















Danh sách bình luận