a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với \(OA = h,AB = R\) và \(OC = r\), quanh trục Ox (H.4.28).
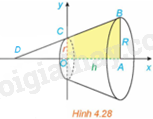
b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h.
Sử dụng kiến thức về công thức tính thể tích của khối tròn xoay để tính: Cho hàm số f(x) liên tục, không âm trên đoạn [a; b]. Khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay. Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm \(x \in \left[ {a;b} \right]\) được một hình tròn có bán kính f(x). Thể tích của khối tròn xoay này là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \).
a)
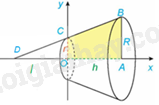
Ta có: \(C\left( {0;r} \right),B\left( {h,R} \right) \Rightarrow \overrightarrow {BC} \left( { - h,r - R} \right) \Rightarrow \overrightarrow n \left( {r - R,h} \right)\)
Phương trình đường thẳng BC là: \(\left( {r - R} \right)x + h\left( {y - r} \right) = 0 \Leftrightarrow y = \frac{{hr + \left( {R - r} \right)x}}{h}\)
Thể tích hình cần tính là:
\(V = \pi \int\limits_0^h {{{\left[ {\frac{{hr + \left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {{{\left[ {r + \frac{{\left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {\left[ {{r^2} + \frac{{2r\left( {R - r} \right)x}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^2}}}{{{h^2}}}} \right]dx} \)
\( = \pi \left( {{r^2}x + \frac{{r\left( {R - r} \right){x^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^3}}}{{3{h^2}}}} \right)\left| \begin{array}{l}h\\0\end{array} \right. = \pi \left( {{r^2}h + \frac{{r\left( {R - r} \right){h^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{h^3}}}{{3{h^2}}}} \right)\)
\( = \pi \left( {{r^2}h + r\left( {R - r} \right)h + \frac{{{{\left( {R - r} \right)}^2}h}}{3}} \right) = \pi \left( {{r^2}h + rRh - {r^2}h + \frac{{{R^2}h}}{3} - \frac{{2rRh}}{3} + \frac{{{r^2}h}}{3}} \right)\)
\( = \pi \left( {\frac{{rRh}}{3} + \frac{{{R^2}h}}{3} + \frac{{{r^2}h}}{3}} \right) = \frac{1}{3}\pi h\left( {{R^2} + rR + {r^2}} \right)\)
b) Khi \(r = 0\) thì khối nón cụt trở thành khối nón có chiều cao h và bán kính đáy R. Do đó, thể tích khối nón là: \(V = \frac{1}{3}\pi {R^2}h\).

Các bài tập cùng chuyên đề
Bài 1 :
Gọi $V$ là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x \), \(y = 0\) và $x = 4$ quanh trục $Ox$ . Đường thẳng \(x = a\) \((0 < a < 4)\) cắt đồ thị hàm số \(y = \sqrt x \) tại $M$ (hình vẽ bên).

Gọi ${V_1}$ là thể tích khối tròn tạo thành khi quay quanh tam giác $OMH$ quanh trục $Ox$. Biết rằng \(V = 2{V_1}\) . Khi đó:
-
A.
\(a = 2\sqrt 2 \)
-
B.
$a = \dfrac{5}{2}$
-
C.
\(a = 2\)
-
D.
$a = 3$
Bài 2 :
Thể tích khối tròn xoay thu được khi quay quanh trục \(Ox\) hình phẳng giới hạn bởi đồ thị hàm số \(y=\frac{\sqrt{3x+1}}{x+1},\) trục hoành và đường thẳng \(x=1\) là
-
A.
\(\pi .3\ln 3.\)
-
B.
\(\pi .\left( 3\ln 3-2 \right).\)
-
C.
\(3\ln 3-1.\)
-
D.
\(\pi .\left( 3\ln 3-1 \right).\)
Bài 3 :
Xét hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right) = \frac{1}{2}x\), trục hoành và hai đường thẳng \(x = 0,x = 4\). Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).
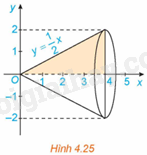
a) Tính thể tích V của khối nón.
b) Chứng minh rằng khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là \(S\left( x \right) = \pi {f^2}\left( x \right)\). Tính \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} \) và so sánh với V.
Bài 4 :
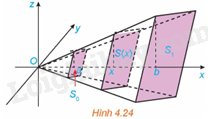
Tính thể tích của khối chóp cụt đều có diện tích hai đáy là \({S_o},{S_1}\) và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.
Bài 5 :
Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng \(x = a\) và \(x = b\left( {a < b} \right)\) (H.4.20).
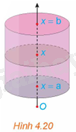
a) Tính thể tích V của hình trụ.
b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x \(\left( {a \le x \le b} \right)\). Từ đó tính \(\int\limits_a^b {S\left( x \right)dx} \) và so sánh với V.
Bài 6 :
Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox: \(y = 2x - {x^2},y = 0,x = 0,x = 2\).
Bài 7 :
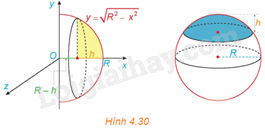
Khối chỏm cầu có bán kính R và chiều cao h\(\left( {0 < h \le R} \right)\) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình \(y = \sqrt {{R^2} - {x^2}} \), trục hoành và hai đường thẳng \(x = R - h,x = R\) xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.
Bài 8 :
Cho tam giác vuông OAB có cạnh \(OA = a\) nằm trên trục Ox và \(\widehat {AOB} = \alpha \left( {0 < \alpha \le \frac{\pi }{4}} \right)\). Gọi \(\beta \) là khối tròn xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox (H.4.31).
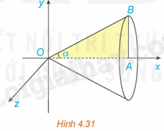
a) Tính thể tích V của \(\beta \) theo a và \(\alpha \).
b) Tìm \(\alpha \) sao cho thể tích V lớn nhất.
Bài 9 :
Cho hình phẳng (S) giới hạn bởi đồ thị hàm số \(y = \sqrt {1 - {x^2}} \), trục hoành và hai đường thẳng \(x = - 1,x = 1\). Thể tích của khối tròn xoay khi quay (S) quanh Ox là
A. \(\frac{{3\pi }}{4}\).
B. \(\frac{{3\pi }}{2}\).
C. \(\frac{{2\pi }}{3}\).
D. \(\frac{{4\pi }}{3}\).
Bài 10 :
Tính thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox:
a) \(y = 1 - {x^2},y = 0,x = - 1,x = 1\);
b) \(y = \sqrt {25 - {x^2}} ,y = 0,x = 2,x = 4\).
Bài 11 :
Nghệ thuật làm gốm có lịch sử phát triển lâu đời và vẫn còn tồn tại cho đến ngày nay. Giả sử một bình gốm có mặt trong bình là một mặt tròn xoay sinh ra khi cho phần đồ thị của hàm số \(y = \frac{1}{{175}}{x^2} + \frac{3}{{35}}x + 5\left( {0 \le x \le 30} \right)\) (x, y tính theo cm) quay tròn quanh bệ gồm có trục trùng với trục hoành Ox. Hỏi để hoàn thành bình gốm đó ta cần sử dụng bao nhiêu \(c{m^3}\) đất sét, biết rằng bình gốm đó có độ dày không đổi là 1 cm.
Bài 12 :
Gọi (H) là hình phẳng giới hạn bởi các đường \(y = 2\sqrt x ,y = 0,x = 0\) và \(x = 4\). Thể tích V của khối tròn xoay sinh ra khi quay hình phẳng (H) quanh trục Ox là
A. \(V = 32\).
B. \(V = 32\pi \).
C. \(V = \frac{{32}}{3}\).
D. \(V = \frac{{32\pi }}{3}\).
Bài 13 :
Gọi (H) là hình phẳng giới hạn bởi các đường \(y = - {x^2} + 2x;y = 0,x = 0\) và \(x = 2\). Tính thể tích của khối tròn xoay thu được khi quay hình phẳng (H) xung quanh trục Ox.
Bài 14 :
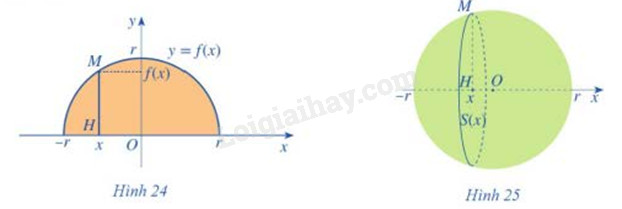
Xét hình tròn tâm O, bán kính r (Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y = f(x)
a) Tìm hàm số y = f(x)
b) Quay nửa hình tròn đó quanh trục hoành, ta nhận được hình cầu tâm O bán kính r (Hình 25). Xét điểm M(x;f(x)) \(( - r \le x \le r)\) nằm trên nửa đường tròn tâm O bán kính r. Gọi H(x;0) là hình chiếu của điểm M trên trục Ox. Khi quay nửa hình tròn quanh trục hoành, đoạn thẳng HM tạo nên một hình tròn tâm H bán kính f(x)
Tính diện tích S(x) của hình tròn đó theo f(x)
Từ đó, sử dụng công thức tính thể tích vật thể, hãy tính thể tích V của hình cầu tâm O bán kính r
Bài 15 :
Cắt khối lập phương có cạnh bằng 1 bởi một mặt phẳng tùy ý vuông góc với trục Ox tại x, với ta nhận được hình phẳng có diện tích là S(x) (Hình 17)
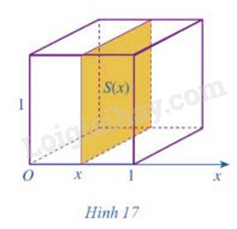
a) Tính S(x)
b) So sánh thể tích khối lập phương đó với \(\int\limits_0^1 {S(x)dx} \)
Bài 16 :
Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số \(f(x) = \sqrt x \), trục hoành và hai đường thẳng x = 0, x = 2 quay quanh trục Ox là:
A. \(\pi \int\limits_0^2 {\sqrt x dx} \)
B. \(\pi \int\limits_0^2 {xdx} \)
C. \(\int\limits_0^2 {\sqrt x dx} \)
D. \(\int\limits_0^2 {xdx} \)
Bài 17 :
Cho đồ thị hàm số \(y = \frac{1}{x}\) và khối tròn xoay như Hình 31.
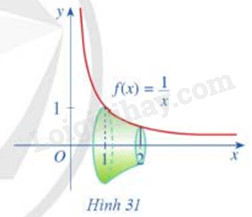
a) Hình phẳng được giới hạn bởi các đường nào để khi xoay quanh trục Ox ta được khối tròn xoay như Hình 31?
b) Tính thể tích khối tròn xoay đó.
Bài 18 :
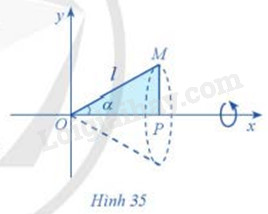
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Giả sử \(\widehat {POM} = \alpha ,OM = l(0 \le \alpha \le \frac{\pi }{3};l > 0)\). Gọi \({\rm N}\) là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (Hình 35). Tính thể tích của \({\rm N}\) theo \(\alpha \) và \(l\)
Bài 19 :
Sau khi đo kích thước của thùng rượu vang (Hình 36), bạn Quân xác định thùng rượu vang có dạng hình tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số \(y = - 0,011{x^2} - 0,071x + 40\), trục Ox và hai đường thẳng x = -35, x = 35 quay quanh trục Ox. Tính thể tích thùng rượu đó, biết đơn vị trên mỗi trục tọa độ là centimet

Bài 20 :
Cho khối tròn xoay như Hình 39.
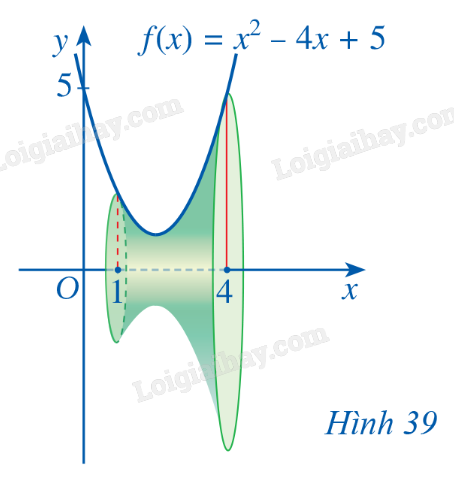
a) Hình phẳng được giới hạn bởi các đường nào để khi quay quanh trục Ox ta được khối tròn xoay như Hình 39.
b) Tính thể tích khối tròn xoay đó.
Bài 21 :
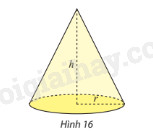
Sử dụng tích phân, tính thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\). (hình 16)
Bài 22 :
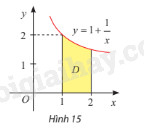
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 1 + \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) (hình 15). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
Bài 23 :
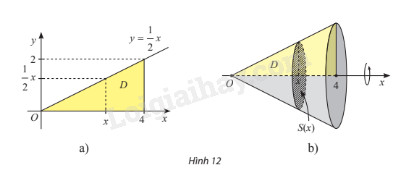
Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = \frac{1}{2}x\), trục hoành và đường thẳng \(x = 4\) (hình 12a). Quay hình \(D\) xung quanh trục \(Ox\) thì được một khối nón, kí hiệu là \(N\). (hình 12b)
a) Cắt khối \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le 4} \right)\) thì mặt cắt là hình gì? Tính diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Sử dụng công thức tính thể tích hình khối, tính thể tích của khối nón \(N\).
Bài 24 :
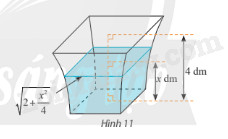
Một bình chứa nước có dạng như hình 11. Biết rằng khi nước ở trong bình có chiều cao \(x\) (dm) \(\left( {0 \le x \le 4} \right)\) thì mặt nước là hình vuông có cạnh \(\sqrt {2 + \frac{{{x^2}}}{4}} \) (dm). Tính dung tích của bình.
Bài 25 :
Trong không gian, cho hình chóp \(O.ABCD\) có đáy là hình vuông cạnh \(a\), \(OA \bot \left( {ABCD} \right)\), \(OA = h\). Đặt trục số \(Ox\) như hình 8. Một mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 < x \le h} \right)\), cắt hình chóp \(O.ABCD\) theo mặt cắt là hình vuông \(A'B'C'D'\). Kí hiệu \(S\left( x \right)\) là diện tích của hình vuông \(A'B'C'D'\).
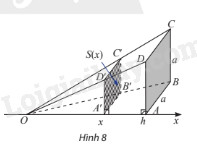
a) Tính \(S\left( x \right)\) theo \(a\), \(h\) và \(x\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và so sánh với thể tích của khối chóp \(O.ABCD\).
Bài 26 :
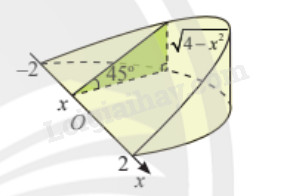
Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( { - 2 \le x \le 2} \right)\), mặt cắt là tam giác vuông có một góc \({45^o}\) và độ dài một cạnh góc vuông là \(\sqrt {4 - {x^2}} \) (dm). Tính thể tích của vật thể.
Bài 27 :
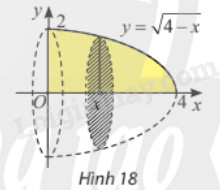
Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {4 - x} \) \(\left( {x \le 4} \right)\), trục tung và trục hoành (hình 18). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
Bài 28 :
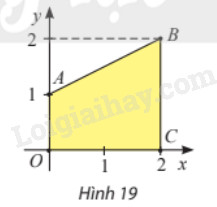
Trong mặt phẳng toạ độ \(Oxy\), cho hình thang \(OABC\) có \(A\left( {0;1} \right)\), \(B\left( {2;2} \right)\) và \(C\left( {2;0} \right)\) (hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang \(OABC\) quanh trục \(Ox\).
Bài 29 :
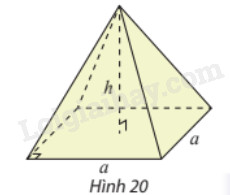
Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng \(a\) và chiều cao bằng \(h\).
Bài 30 :
Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {x + 1} \), trục tung, trục hoành và đường thẳng \(x = 2\). Thể tích của khối tròn xoay khi quay \(D\) quanh trục hoành bằng
A. \(6\pi \)
B. \(2\pi \)
C. \(3\pi \)
D. \(4\pi \)


















Danh sách bình luận