a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.

a) Sử dụng kiến thức về đạo hàm của hàm số lượng giác để tính:
\(\left( {\sin x} \right)' = \cos x,\left( {\cos x} \right)' = - \sin x,\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}},\left( {\cot x} \right)' = \frac{{ - 1}}{{{{\sin }^2}x}}\)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
a)

b)
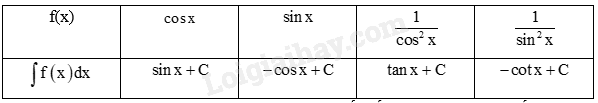

Các bài tập cùng chuyên đề
Bài 1 :
Tìm:
a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} \);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} \).
Bài 2 :
Tìm:
a) \(\int {\left( {2\cos x - \frac{3}{{{{\sin }^2}x}}} \right)} dx\);
b) \(\int {4{{\sin }^2}\frac{x}{2}} dx\);
c) \(\int {{{\left( {\sin \frac{x}{2} - \cos \frac{x}{2}} \right)}^2}} dx\);
d) \(\int {\left( {x + {{\tan }^2}x} \right)} dx\).
Bài 3 :
Tìm một nguyên hàm F(x) của hàm số \(f\left( x \right) = 2\cos x + \frac{1}{{{{\sin }^2}x}}\) thỏa mãn điều kiện \(F\left( {\frac{\pi }{4}} \right) = - 1\).
Bài 4 :
a) Hàm số \(y = - \cos x\) có là nguyên hàm của hàm số \(y = \sin x\)
b) Hàm số \(y = \sin x\) có là nguyên hàm của hàm số \(y = \cos x\)
c) Với \(x \notin k\pi (k \in \mathbb{Z})\), hàm số \(y = \cot x\) có là nguyên hàm của hàm số \(\frac{1}{{{{\sin }^2}(x)}}\) hay không?
d) Với \(x \notin \frac{\pi }{2} + k\pi (k \in \mathbb{Z})\), hàm số \(y = \tan x\) có là nguyên hàm của hàm số \(\frac{1}{{{{\cos }^2}(x)}}\) hay không?
Bài 5 :
\(\int {(2\sin x - 3\cos x)dx} \) bằng:
A. \(2\cos x - 3\sin x + C\)
B. \(2\cos x + 3\sin x + C\)
C. \( - 2\cos x + 3\sin x + C\)
D. \( - 2\cos x - 3\sin x + C\)
Bài 6 :
Nguyên hàm của hàm số \(f(x) = 1 - {\tan ^2}(x)\) bằng:
A. \(2 - \tan x + C\)
B. \(2x - \tan x + C\)
C. \(x - \frac{{{{\tan }^3}x}}{3} + C\)
D. \( - 2\tan x + C\)
Bài 7 :
Tìm nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right) = \cos x\) thoả mãn \(F\left( 0 \right) + F\left( {\frac{\pi }{2}} \right) = 0\).
Bài 8 :
a) Tìm đạo hàm của các hàm số \(y = \sin x\), \(y = - \cos x\), \(y = \tan x\), \(y = - \cot x\).
b) Từ đó, tìm \(\int {\cos xdx} \), \(\int {\sin x} dx\), \(\int {\frac{1}{{{{\cos }^2}x}}dx} \), \(\int {\frac{1}{{{{\sin }^2}x}}dx} \)
Bài 9 :
Tìm nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right) = \frac{1}{{{{\sin }^2}x}}\) thoả mãn \(F\left( {\frac{\pi }{2}} \right) = 1\).
Bài 10 :
Khẳng định nào sau đây đúng?
A. \(\int {\left( {\cos x - 2\sin x} \right)dx} = \sin x + 2\cos x + C\)
B. \(\int {\left( {\cos x - 2\sin x} \right)dx} = - \sin x + 2\cos x + C\)
C. \(\int {\left( {\cos x - 2\sin x} \right)dx} = \sin x - 2\cos x + C\)
D. \(\int {\left( {\cos x - 2\sin x} \right)dx} = - \sin x - 2\cos x + C\)
Bài 11 :
Hàm số \(y = \sin 2x\) là nguyên hàm của hàm số:
A. \(y = \cos 2x\).
B. \(y = 2\cos 2x\).
C. \(y = - \cos 2x\).
D. \(y = \frac{{ - \cos 2x}}{2}\).
Bài 12 :
Xét dao động điều hoà của một chất điểm có vận tốc tức thời tại thời điểm \(t\) là: \(v\left( t \right) = - 0,2\pi \sin \left( {\pi t} \right)\), trong đó, \(t\) tính bằng giây, \(v\left( t \right)\) tính bằng \(m/s\). Tìm phương trình li độ \(x\left( t \right)\), biết \(v\left( t \right)\) là đạo hàm của \(x\left( t \right)\) và \(x\left( 0 \right) = 0,2\left( m \right)\).
Bài 13 :
\(\int {\sin \left( { - x} \right)dx} \) bằng:
A. \(\sin x + C\).
B. \(\cos x + C\).
C. \( - \sin x + C\).
D. \( - \cos x + C\).
Bài 14 :
\(\int {\cos \left( { - x} \right)dx} \) bằng:
A. \(\sin x + C\).
B. \(\cos x + C\).
C. \( - \sin x + C\).
D. \( - \cos x + C\).
Bài 15 :
\(\int {\frac{1}{{{{\sin }^2}\left( { - x} \right)}}dx} \) bằng:
A. \(\tan x + C\).
B. \(\cot x + C\).
C. \( - \tan x + C\).
D. \( - \cot x + C\).
Bài 16 :
\(\int {\frac{1}{{{{\cos }^2}\left( { - x} \right)}}dx} \) bằng:
A. \(\tan x + C\).
B. \(\cot x + C\).
C. \( - \tan x + C\).
D. \( - \cot x + C\).
Bài 17 :
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
Cho hàm số \(f\left( x \right) = \frac{{\sin 3x + \sin x}}{{\sin 2{\rm{x}}}}\).
a) \(f\left( x \right) = \frac{{2\sin \frac{{3x + x}}{2}\cos \frac{{3x - x}}{2}}}{{\sin 2{\rm{x}}}}\).
b) \(f\left( x \right) = 2\cos x\).
c) \(\int {f\left( x \right)dx} = 2\int {\cos xdx} \).
d) \(\int {f\left( x \right)dx} = - 2\sin x + C\).
Bài 18 :
Tìm:
a) \(\int {{x^{\frac{1}{3}}}} dx\);
b) \(\int {\sqrt {\frac{1}{{{x^7}}}} } dx\);
c) \(\int {\frac{1}{{\sqrt[3]{{{x^{\frac{4}{5}}}}}}}} dx\);
d) \(\int {{{\left( {x - \frac{1}{x}} \right)}^2}} dx\);
e) \(\int {\frac{{\left( {x - 3} \right)\left( {x + 1} \right)}}{x}} dx\);
g) \(\int {\left( {3{{\rm{x}}^2} - \frac{4}{x}} \right)\left( {2{\rm{x}} + 5} \right)} dx\).
Bài 19 :
\(\int {\sin xdx} \) bằng
-
A.
sinx + C
-
B.
- cosx + C
-
C.
cosx + C
-
D.
- sinx + C
Bài 20 :
Tìm:
a) \(\int {\frac{{{{\cos }^2}x}}{{1 - \sin x}}dx} \);
b) \(\int {\left( {1 + 3{{\sin }^2}\frac{x}{2}} \right)dx} \);
c) \(\int {\frac{{2{{\cos }^3}x + 3}}{{{{\cos }^2}x}}dx} \).
Bài 21 :
Chọn đáp án đúng.
Hàm số \(y = f\left( x \right)\) có đồ thị đi qua điểm \(\left( {0;2} \right)\) và \(f'\left( x \right) = \cos x - \sin x\). Giá trị của \(f\left( \pi \right)\) là
A. ‒1.
B. 1.
C. 4.
D. 0.
Bài 22 :
Tính đạo hàm của các hàm số sau:
a) \(y = \sin x;\)
b) \(y = - \cos x;\)
c) \(y = \tan x;\)
d) \(y = - \cot x\).
Bài 23 :
Họ các nguyên hàm của hàm số \(f(x) = x + \sin x\) là
-
A.
\({x^2} + \cos x + C\)
-
B.
\({x^2} - \cos x + C\)
-
C.
\(\frac{{{x^2}}}{2} - \cos x + C\)
-
D.
\(\frac{{{x^2}}}{2} + \cos x + C\)
Bài 24 :
Họ các nguyên hàm của hàm số \(f(x) = {x^2} + \cos x\) là
-
A.
\(2x - \sin x + C\)
-
B.
\(\frac{1}{3}{x^3} + \sin x + C\)
-
C.
\(\frac{1}{3}{x^3} - \sin x + C\)
-
D.
\(\frac{1}{3}{x^3} - \sin x + C\)
Bài 25 :
Nguyên hàm của hàm số f(x) = sinx là
-
A.
cosx + C
-
B.
sinx + C
-
C.
-cosx + C
-
D.
-sinx + C
Bài 26 :
Nguyên hàm của hàm số f(x) = 5cosx là
-
A.
5sinx + C
-
B.
5sin2x + C
-
C.
sin5x + C
-
D.
-5sinx + C
Bài 27 :
Tìm nguyên hàm của hàm số \(f(x) = \frac{{1 - {{\sin }^3}x}}{{{{\sin }^2}x}}\).
-
A.
\(\int {f(x)dx} = - \cot x + \cos x + C\)
-
B.
\(\int {f(x)dx} = - \tan x + \cos x + C\)
-
C.
\(\int {f(x)dx} = - \cot x - \cos x + C\)
-
D.
\(\int {f(x)dx} = - \tan x - \cos x + C\)
Bài 28 :
Nguyên hàm của hàm số y = sinx + 2cosx là
-
A.
cosx – 2sinx + C
-
B.
-cosx + 2sinx + C
-
C.
cosx + 2sinx + C
-
D.
-cosx – 2sinx + C
Bài 29 :
Mệnh đề nào dưới đây đúng?
-
A.
\(\int {\cos xdx} = \sin x + C\)
-
B.
\(\int {\cos xdx} = - \sin x + C\)
-
C.
\(\int {\cos xdx} = - \cos x + C\)
-
D.
\(\int {\cos xdx} = \frac{1}{2}{\cos ^2}x + C\)
Bài 30 :
Hàm số F(x) = cotx là một nguyên hàm của hàm số nào dưới đây trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\)?
-
A.
\({f_2}\left( x \right) = \frac{1}{{{{\sin }^2}x}}\)
-
B.
\({f_1}\left( x \right) = - \frac{1}{{{{\cos }^2}x}}\)
-
C.
\({f_4}\left( x \right) = \frac{1}{{{{\cos }^2}x}}\)
-
D.
\({f_3}\left( x \right) = - \frac{1}{{{{\sin }^2}x}}\)


















Danh sách bình luận