Tính tổng và hiệu của hai đa thức \(P = {x^2}y + {x^3} - x{y^2} + 3\) và \(Q = {x^3} + x{y^2} - xy - 6\).
Muốn cộng (hay trừ) hai đa thức, ta nối hai đa thức đã cho bởi dấu (+) (hoặc dấu (-)) rồi bỏ dấu ngoặc (nếu có) và thu gọn đa thức nhận được.
Chú ý trước dấu ngoặc là dấu (-) thì khi phá ngoặc, ta đổi dấu tất cả các hạng tử trong dấu ngoặc.
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
\(\begin{array}{l}P + Q = {x^2}y + {x^3} - x{y^2} + 3 + {x^3} + x{y^2} - xy - 6\\ = \left( {{x^3} + {x^3}} \right) + {x^2}y + \left( { - x{y^2} + x{y^2}} \right) - xy + \left( {3 - 6} \right)\\ = 2{x^3} + {x^2}y - xy - 3\\P - Q = {x^2}y + {x^3} - x{y^2} + 3 - \left( {{x^3} + x{y^2} - xy - 6} \right)\\ = {x^2}y + {x^3} - x{y^2} + 3 - {x^3} - x{y^2} + xy + 6\\ = \left( {{x^3} - {x^3}} \right) + {x^2}y + \left( { - x{y^2} - x{y^2}} \right) + xy + \left( {3 + 6} \right)\\ = - 2x{y^2} + {x^2}y + xy + 9\end{array}\)
Các bài tập cùng chuyên đề
Cho hai đa thức \(G = {x^2}y - 3xy - 3\) và \(H = 3{x^2}y + xy - 0,5x + 5\).
Hãy tính G+H và G-H.
Rút gọn và tính giá trị của biểu thức sau tại x=2 và y=-1.
\(K = \left( {{x^2}y + 2x{y^3}} \right) - \left( {7,5{x^3}{y^2} - {x^3}} \right) + \left( {3x{y^3} - {x^2}y + 7,5{x^3}{y^2}} \right)\)
Rút gọn biểu thức:
a) \(\left( {x - y} \right) + \left( {y - z} \right) + \left( {z - x} \right)\);
b) \(\left( {2x - 3y} \right) + \left( {2y - 3z} \right) + \left( {2z - 3x} \right)\).
Cho hai đa thức \(A = 2{x^2}y + 3xyz - 2x + 5\) và \(B = 3xyz - 2{x^2}y + x - 4\).
a) Tìm các đa thức A+B và A-B.
b) Tính giá trị của các đa thức A và A+B tại x=0,5;y=-2 và z=1.
Cho các biểu thức:
\(\dfrac{4}{5}x;\left( {\sqrt 2 - 1} \right)xy; - 3x{y^2};\dfrac{1}{2}{x^2}y;\dfrac{1}{x}{y^3}; - xy + \sqrt 2 ;\dfrac{{ - 3}}{2}{x^2}y;\dfrac{{\sqrt x }}{5}.\)
a) Trong các biểu thức đã cho, biểu thức nào là đơn thức? Biểu thức nào không là đơn thức?
b) Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.
c) Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.
Cho hai đa thức:
\(A = 7xy{z^2} - 5x{y^2}z + 3{x^2}yz - xyz + 1;\\B = 7{x^2}yz - 5x{y^2}z + 3xy{z^2} - 2.\)
a) Tìm đa thức C sao cho A-C=B;
b) Tìm đa thức D sao cho A+D=B;
c) Tìm đa thức E sao cho E-A=B;
Cho ba đa thức:
\(M = 3{x^3} - 4{x^2}y + 3x - y;N = 5xy - 3x + 2;P = 3{x^3} + 2{x^2}y + 7x - 1.\)
Tính M + N - P và M - N - P.
Gọi T là tổng, H là hiệu của hai đa thức \(3{x^2}y - 2x{y^2} + xy\) và \( - 2{x^2}y + 3x{y^2} + 1\). Khi đó:
A. \(T = {x^2}y - x{y^2} + xy + 1\) và \(H = 5{x^2}y - 5x{y^2} + xy - 1\).
B. \(T = {x^2}y + x{y^2} + xy + 1\) và \(H = 5{x^2}y - 5x{y^2} + xy - 1\)
C. \(T = {x^2}y + x{y^2} + xy + 1\) và \(H = 5{x^2}y - 5x{y^2} - xy - 1\)
D. \(T = {x^2}y + x{y^2} + xy - 1\) và \(H = 5{x^2}y + 5x{y^2} + xy - 1\)
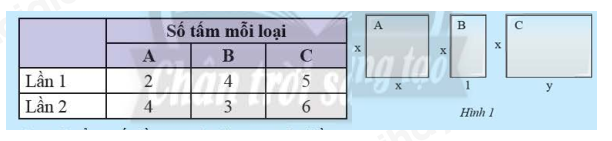
Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng \(A\), \(B\) và \(C\) với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá \(a\) đồng/\({m^2}\). Tại đây có hai lần nhập vật liệu như bảng sau:
a) Tính tổng số tiền mua kính của cả hai lần.
b) Số tiền lần 2 nhiều hơn lần 1 bao nhiêu?
Cho hai đa thức \(M = 1 + 3xy - 2{x^2}{y^2}\) và \(N = x - xy + 2{x^2}{y^2}\). Tính \(M + N\) và \(M - N\).
Tính:
a) \(x + 2y + \left( {x - y} \right)\)
b) \(2x - y - \left( {3x - 5y} \right)\)
c) \(3{x^2} - 4{y^2} + 6xy + 7 + \left( { - {x^2} + {y^2} - 8xy + 9x + 1} \right)\)
d) \(4{x^2}y - 2x{y^2} + 8 - \left( {3{x^2}y + 9x{y^2} - 12xy + 6} \right)\)
Tính giá trị của biểu thức:
a) \(3{x^2}y - \left( {3xy - 6{x^2}y} \right) + \left( {5xy - 9{x^2}y} \right)\) tại \(x = \frac{2}{3}\), \(y = - \frac{3}{4}\)
b) \(x\left( {x - 2y} \right) - y\left( {{y^2} - 2x} \right)\) tại \(x = 5\), \(y = 3\)
Cho đa thức \(P = 3{x^2}y - 2x{y^2} - 4xy + 2\).
a) Tìm đa thức \(Q\) sao cho \(Q - P = - 2{x^3}y + 7{x^2}y + 3xy\)
b) Tìm đa thức \(M\) sao cho \(P + M = 3{x^2}{y^2} - 5{x^2}y + 8xy\)
Với ba đa thức: \(A = {x^2} - 2{\rm{x}}y + {y^2};B = 2{{\rm{x}}^2} - {y^2};C = {x^2} - 3{\rm{x}}y\)(ở trong ví dụ 3). Hãy tính:
a) B – C
b) (B – C) + A
Cho hai đa thức \(P = 4x{y^2} + 6x - 3\) và \(Q = 2x{y^2} - 5x + 1\)
- Viết các biểu thức \(P + Q\) và \(P - Q\)
- Thu gọn \(P + Q\) và \(P - Q\)
Tính tổng và hiệu của hai đa thức \(P = x{y^3} - {x^3} + 2x - 3y\) và \(Q = 2x{y^3} + 6{x^3} - 7x + 1\)
Cho hai đa thức \(P = {x^3}{y^4} - 4{x^2}{y^2} - 4x + 6\)vvà \(Q = 5{x^2}{y^2} - 3{x^3}{y^4} + x - 1\). Tính \(P + Q\) và \(P - Q\).
Cho hai đa thức \(A = {x^2} - 3xy + 2{y^2}\)và \(B = {y^2} + 2xy + {x^2} + 1\)
a) Tìm đa thức \(C\) sao cho \(C = A + B\)
b) Tìm đa thức \(D + A = B\)
Cho hai đa thức: \(A = {x^7} - 4{x^3}{y^2} - 5xy + 7;B = {x^7} + 5{x^3}{y^2} - 3xy - 3\)
a) Tìm đa thức \(C\) sao cho \(C = A + B\)
b) Tìm đa thức \(D\) sao cho \(A + D = B\)
Tính:
a) \(7x + \left( { - 3xy + 5x} \right)\);
b) \(4x - 3y - \left( {3 + 3x - y} \right)\);
c) \(2xy - 4xy - \left( {y - 3xy} \right)\);
d) \(\left( {{x^2}y - 3x{y^2} - {y^2}} \right) + \left( {5x{y^2} - 4{y^2} + 5{x^2}y} \right)\).
Tính:
a) \(2a + 4b + \left( { - 4b + 5a} \right) - \left( {6a - 9b} \right)\);
b) \(6a - \left[ {b + 3a - \left( {4a - b} \right)} \right]\).
Tìm tổng \(P + Q\) và hiệu \(P - Q\) của hai đa thức:
\(P = 4{x^2}{y^2} - 3x{y^3} + 5{x^3}y - xy + 2x - 3\)
\(Q = - 4{x^2}{y^2} - 4x{y^3} - {x^3}y + xy + y + 1\)
Cho ba đa thức:
\(M = 3{x^3} - 5{x^2}y + 5x - 3y\)
\(N = 4xy - 4x + y\)
\(P = 3{x^3} + {x^2}y + x + 1\).
Tính \(M + N - P\) và \(M - N - P\).
Tính tổng và hiệu của hai đa thức \(P = {x^2}y + {x^3} - x{y^2} + 3\) và \(Q = {x^3} + x{y^2} - xy - 6\) .
Cho hai đa thức \(A = 2{x^2}y + 3xyz - 2x + 5\) và \(B = 3xyz - 2{x^2}y + x - 4\) .
a) Tìm các đa thức \(A + B\) và \(A - B\) ;
b) Tính giá trị của các đa thức A và \(A + B\) tại \(x = 0,5;y = - 2\) và \(z = 1\) .
Cho hai đa thức:
\(P = 4{x^3}y{z^2} - 3{x^2}y - 2{x^3}y{z^2} + {x^2}y - 2xy + y + 5\);
\(Q = - {x^3}y{z^2} - 2{x^2}y + 3 + 3{x^3}y{z^2} + xy - y + 2\).
a) Thu gọn và xác định bậc của mỗi đa thức P và Q.
b) Xác định bậc của mỗi đa thức \(P + Q\) và \(P - Q\).
Cho đa thức \(P = 5{x^2}y - 2x{y^2} + xy - x + y - 2\).
a) Tìm đa thức Q, biết rằng \(P + Q = \left( {x + y} \right)\left( {2xy + 2{y^2} - 1} \right)\).
b) Tìm đa thức R, biết rằng \(P - R = - xy\left( {x - y} \right)\).
Cho hai đa thức: \(M = 23{x^{23}}y - 22x{y^{23}} + 21y - 1\) và \(N = - 22x{y^3} - 42y - 1\)
a) Tính giá trị của mỗi đa thức \(M,N\) tại \(x = 0;y = - 2\)
b) Tính \(M + N;M - N\)
c) Tìm đa thức \(P\) sao cho \(M - N - P = 63y + 1\)
Cho hai đa thức
\(A = 7xy{z^2}-5x{y^2}z + 3{x^2}yz-xyz + 1;\\B = 7{x^2}yz-5x{y^2}z + 3xy{z^2}-2.\)
a) Tìm đa thức C sao cho \(A-C = B\) .
b) Tìm đa thức D sao cho \(A + D = B\) .
c) Tìm đa thức E sao cho \(E-A = B\) .
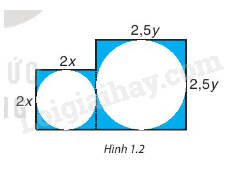
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimét và y centimét. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu biết miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (centimét) như hình bên. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?
