Dựng đường phân giác góc xOy:
• Vẽ đường tròn (O) cắt hai cạnh của góc xOy tại A và B;
• Vẽ hai đường tròn tâm A và B có cùng bán kính cắt nhau tại điểm C khác điểm O. Khi đó, OC là tia phân giác của góc xOy.
Dựng đường trung trực của đoạn thẳng AB: Vẽ hai đường tròn tâm A và tâm B có cùng bán kính lớn hơn \(\frac{1}{2}AB\) cắt nhau tại hai điểm M, N. Khi đó MN là đường trung trực của AB.
Dựng đường thẳng qua điểm A và vuông góc với đường thẳng d:
• Vẽ đường tròn tâm A cắt d tại hai điểm B và C;
• Vẽ hai đường tròn tâm B và C có cùng bán kính cắt nhau tại điểm D khác A. Khi đó AD là đường thẳng cần dựng.
Vì sao các cách dựng trên cho ta đường phân giác, đường trung trực và đường thẳng vuông góc cần dựng?
+ Chứng minh cách dựng đường phân giác: Chứng minh \(\Delta BOC = \Delta AOC\left( {c.c.c} \right)\), suy ra \(\widehat {BOC} = \widehat {AOC}\) nên OC là tia phân giác của góc xOy.
+ Chứng minh đường trung trực: Chứng minh \(MA = MB,NA = NB\) nên M, N thuộc đường trung trực của AB, do đó, MN là đường trung trực của AB.
+ Chứng minh đường thẳng vuông góc: Chứng minh \(AB = AC,BD = DC\) nên A, D thuộc đường trung trực của BC. Do đó, AD là đường trung trực của BC nên AD vuông góc với BC.
+ Chứng minh cách dựng đường phân giác:
Vì B, A thuộc (O) nên \(OA = OB\).
Vì đường tròn tâm A và B có cùng bán kính và cắt nhau tại C nên \(CB = CA\).
\(\Delta \)BOC và \(\Delta \)AOC có: \(OA = OB\), \(CB = CA\), OC chung nên \(\Delta BOC = \Delta AOC\left( {c.c.c} \right)\), do đó, \(\widehat {BOC} = \widehat {AOC}\) nên OC là tia phân giác của góc xOy.
+ Chứng minh đường trung trực: Vì hai đường tròn tâm A và tâm B có cùng bán kính và cắt nhau tại M và N nên \(MA = MB,NA = NB\). Do đó, hai điểm M, N thuộc đường trung trực của AB, do đó, MN là đường trung trực của AB.
+ Chứng minh đường thẳng vuông góc:
Vì B, C thuộc (A) nên \(AB = AC\), suy ra A thuộc đường trung trực của BC.
Vì hai đường tròn tâm B và C có cùng bán kính cắt nhau tại điểm D khác A nên \(BD = DC\), suy ra D thuộc đường trung trực của BC.
Vậy AD là đường trung trực của BC. Do đó, đường thẳng AD vuông góc với BC.

Các bài tập cùng chuyên đề
Bài 1 :

Bài 2 :

Bài 3 :

Bài 4 :
Vẽ một hình trụ và một hình nón có chung đáy và đỉnh của hình nón nằm trên mặt đáy còn lại của hình trụ.
Bài 5 :
a) Vẽ đường tròn tâm O, bán kính R = 5 cm theo Cách 2.
b) Vẽ tam giác MNP và vẽ đường tròn ngoại tiếp theo Cách 4.
Bài 6 :
a) Vẽ đường tròn tâm J, bán kính r = 4 cm theo Cách 2 và tính diện tích hình tròn vừa vẽ được.
b) Vẽ điểm O, đoạn thẳng AB và đường tròn tâm O bán kính bằng AB theo Cách 3. Tính diện tích hình tròn vừa vẽ được.
Bài 7 :
Vẽ tứ giác A’B’C’D’ có được qua phép quay ngược chiều tâm O tứ giác ABCD.
Bài 8 :
a) Tạo lập hình nón.
b) Tạo lập hình cầu.
Bài 9 :
Hãy cho biết các tam giác đều vẽ thêm được trong Bước 2 và Bước 3 có bằng nhau không. Giải thích.
Bài 10 :
Hãy kiểm tra xem các tam giác vẽ trong hoạ tiết có phải tam giác đều hay không?
Bài 11 :
Dùng phần mềm GeoGebra để vẽ các hoạ tiết trang trí sau:
Bài 12 :
Em hãy tìm thêm các hình ảnh về các chi tiết được chắp nối trơn trên thực tế.
Bài 13 :
Vẽ chắp nối trơn hai tia Ox và Oy tại điểm A thuộc Ox:
Bước 1: Dựng đường phân giác Oz của góc xOy và đường thẳng qua A vuông góc với Ox. Hai đường thẳng cắt nhau tại M.
Bước 2: Dựng đường thẳng qua M vuông góc với Oy cắt tia Oy tại B. Vẽ đường tròn tâm M đi qua A ta được cung AB nối trơn với hai tia Ox và Oy.
Vì sao với cách dựng như trên thì đường tròn (M; MA) tiếp xúc với cả hai tia Ox và Oy?
Bài 14 :
Sử dụng phương pháp nối trơn hai đường thẳng để hoàn thiện phác thảo bên trái và trang trí thành bản vẽ thiết kế ngã tư đường như trong Hình 5.80
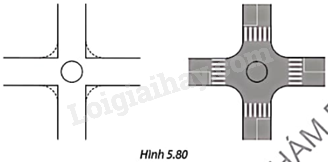
Bài 15 :
Nối trơn đường thẳng xy và đường tròn (O) tại điểm A thuộc (O).
Bước 1: Vẽ tiếp tuyến của đường tròn (O) tại A, cắt xy tại điểm M.
Bước 2: Nối trơn tiếp tuyến Mz và tia My tại điểm A theo các bước ở Hoạt động 2, ta được đường nối cần dựng.
Vì sao với cách dựng như trên thì đường tròn (I; IA) tiếp xúc với đường tròn (O) và đường thẳng xy? Trong trường hợp nào hai đường tròn (O) và (I) tiếp xúc ngoài, trong trường hợp nào hai đường tròn tiếp xúc trong?
Bài 16 :
Sử dụng phương pháp nối trơn đường thẳng với đường tròn để hoàn thiện phác thảo bên trái và tô màu thành hoa văn hình trái tim như trong Hình 5.81.
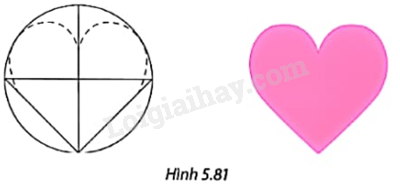
Bài 17 :
Nối trơn hai đường tròn (O) và (I) từ điểm A thuộc (O).
Bước 1: Xác định điểm J trên bán kính OA sao cho AJ bằng bán kính của (I).
Bước 2: Dựng đường trung trực của IJ cắt đường thẳng OA tại M.
Bước 3: Xác định giao điểm B của MI và đường tròn (I). Vẽ đường tròn tâm M đi qua A, ta được cung AB là đường nối trơn cần dựng.
Vì sao với cách dựng như trên thì \(MA = MB\) và đường tròn (M; MA) tiếp xúc với cả hai đường tròn (O) và (I)?
Bài 18 :
Sử dụng phương pháp nối trơn đường tròn với đường tròn ở trên để hoàn thiện phác thảo bên trái và trang trí thành thiết kế hồ bơi trong Hình 5.82.
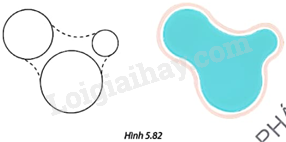
Bài 19 :
Sử dụng các phương pháp dựng hình và chắp nối trơn như trên để thực hiện một thiết kế hoặc mẫu hoa văn trang trí tùy ý. Trình bày ý tưởng và mẫu thiết kế trước lớp.


















Danh sách bình luận