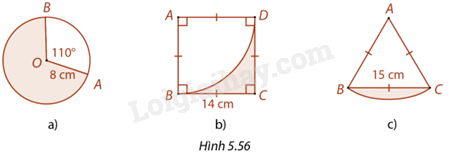
Tính chu vi và diện tích phần được tô màu trong mỗi trường hợp ở Hình 5.56. Làm tròn kết quả đến hàng phần mười.
Công thức tính độ dài cung \({n^o}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\).
Công thức tính diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
a) Góc AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung AB nhỏ là bằng 110 độ.
Khi đó, số đo cung AB lớn bằng:
\({360^o} - {110^o} = {250^o}\).
Phần được tô màu là hình quạt tâm O, cung lớn AB nên
+ Diện tích phần tô màu là:
\(S = \frac{{\pi {{.8}^2}.250}}{{360}} = \frac{{400\pi }}{9} \approx 139,6\left( {c{m^2}} \right)\)
+ Độ dài cung AB lớn là:
\({l_{AB}} = \frac{{\pi .8.250}}{{180}} = \frac{{100\pi }}{9}\left( {cm} \right)\)
+ Chu vi hình được tô màu là:
\(C = OA + OB + {l_{AB}} = 8 + 8 + \frac{{100\pi }}{9} = 16 + \frac{{100\pi }}{9} \approx 50,9\left( {cm} \right)\)
b) Diện tích hình vuông ABCD là:
\({S_{ABCD}} = {14^2} = 196\left( {c{m^2}} \right)\)
Phần không tô màu là \(\frac{1}{4}\) hình tròn bán kính 14cm nên diện tích phần không tô màu là: \({S_1} = \frac{1}{4}{.5^2}.\pi = \frac{{25}}{4}\pi \left( {c{m^2}} \right)\).
Diện tích phần tô màu là:
\(S = {S_{ABCD}} - {S_1} = 196 - \frac{{25\pi }}{4} \approx 176,4\left( {c{m^2}} \right)\)
Độ dài cung BD là:
\({l_{BD}} = \frac{{\pi .14.90}}{{180}} = 7\pi \left( {cm} \right)\)
Chu vi phần được tô màu là:
\(C = DC + CB + {l_{BD}} = 14 + 14 + 7\pi = 28 + 7\pi \approx 50\left( {cm} \right)\)
c) Tam giác ABC có: \(AB = BC = CA\) nên tam giác ABC đều. Do đó, \(\widehat {BAC} = {60^o}\) nên hình quạt tâm A, hai bán kính AB, AC có số đo cung BC bằng 60 độ.
Diện tích hình quạt tâm A, cung BC là:
\({S_q} = \frac{{\pi {{.15}^2}.60}}{{360}} = \frac{{75\pi }}{2}\left( {c{m^2}} \right)\)
Diện tích tam giác đều ABC cạnh 15cm là:
\({S_{ABC}} = \frac{{{{15}^2}\sqrt 3 }}{4} = \frac{{225\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Do đó, diện tích phần được tô màu là:
\(S = {S_q} - {S_{ABC}} = \frac{{75\pi }}{2} - \frac{{225\sqrt 3 }}{4} \approx 20,4\left( {c{m^2}} \right)\)
Độ dài cung BC là:
\({l_{BC}} = \frac{{\pi .15.60}}{{180}} = 5\pi \left( {cm} \right)\).
Chu vi phần được tô màu là:
\({l_{BC}} + BC = 5\pi + 15 \approx 30,7\left( {cm} \right)\).

Các bài tập cùng chuyên đề
Bài 1 :
Em hãy tìm một số hình ảnh của hình quạt tròn và hình vành khuyên trong thực tế
Bài 2 :
Cho đường tròn (O; 5 cm).
a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5 cm.
b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm).
c) Tính số đo và độ dài của cung nhỏ AB.
d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.
Bài 3 :
Cho đường tròn (O) đường kính BC và điểm A (khác B và C).
a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì nằm trên (O).
b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.
c) Với cùng giả thiết câu b), tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng BC = 6 cm.
Bài 4 :
Cho AB là một dây bất kì (không phải là đường kính) của đường tròn (O; 4 cm). Gọi C và D lần lượt là các điểm đối xứng với A và B qua tâm O.
a) Hai điểm C và D có nằm trên đường tròn (O) không? Vì sao?
b) Biết rằng ABCD là một hình vuông. Tính độ dài cung lớn AB và diện tích hình quạt tròn tạo bởi hai bán kính OA và OB.
Bài 5 :
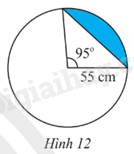
Tính diện tích hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung số đo là 95o. (Hình 12).
Bài 6 :
Một máy kéo nông nghiệp có đường kính bánh xe sau là 124 cm và đường kính bánh xe trước là 80 cm. Hỏi sau khi bánh xe sau lăn được 20 vòng thì bánh xe trước lăn được bao nhiêu vòng?

Bài 7 :
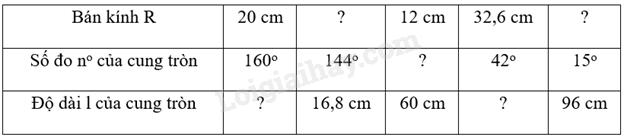
Hãy hoàn thành bảng số liệu sau và vở (lấy \(\pi \approx 3,14\) và làm tròn kết quả đến hàng phần mười)
Bài 8 :
Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC.
a) Chứng minh rằng hai đường tròn (O) và (O’) tiếp xúc ngoài B.
b) Gọi H là trung điểm AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi.
c) DC cắt đường tròn (O’) tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng.
d) Chứng minh rằng HF là tiếp tuyến của đường tròn (O’).
Bài 9 :
Hải đăng Kê Gà tọa lạc tại xã Tân Thành, huyên Hàm Thuận Nam, tỉnh Bình Thuận. Biết ngọn hải đăng cao 65 m so với mặt nước biển. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trông thấy ngọn của hải đăng này?
Cho biết mắt người quan sát ở độ cao 5 m so với mực nước biển và bán kính Trái Đất gần bằng 6400 km.

Bài 10 :
Quan sát các hình 83, 84, 85, 86.
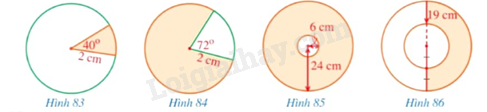
a) Tính diện tích phần được tô màu trong mỗi hình đó.
b) Tính độ dài cung tròn được tô màu xanh ở mỗi hình 83, 84.
Bài 11 :
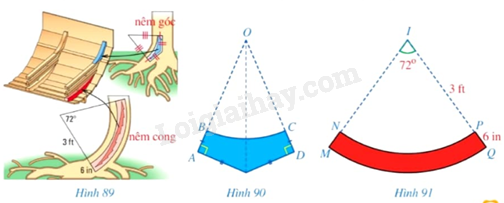
Khi đóng đáy thuyền cho những con thuyền vượt biển, người Vikigns sử dụng hai loại nêm: nêm góc và nêm cong (lần lượt tô màu xanh, màu đỏ trong Hình 89). Mặt cắt \(ABCD\) của nêm góc có dạng hai tam giác vuông \(OAE,ODE\) bằng nhau với cạnh huyền chung và bỏ đi hình quạt tròn \(OBC\)(Hình 90), được làm từ những thân cây mọc thẳng. Mặt cắt \(MNPQ\) của nêm cong có dạng một phần của hình vành khuyên (Hình 91), được làm từ những thân cây cong. Kích thước của nêm cong được cho như ở Hình 91.
a) Diện tích của nêm cong là bao nhiêu centimét vuông (lấy 1 ft = 30,48cm, 1 in = 2,54cm, \(\pi = 3,14\) và làm tròn kết quả đến hàng đơn vị)?
b) Cần phải biết những kích thước nào của nêm góc để tính được diện tích của nêm đó?
Bài 12 :
a) Độ dài cung tròn có số đo \(30^\circ \) của đường tròn có bán kính \(R\) là:
A. \(\frac{{\pi R}}{{180}}\)
B. \(\frac{{\pi R}}{{360}}\)
C. \(30\pi R\)
D. \(\frac{{\pi R}}{6}\)
b) Diện tích của hình quạt tròn tâm O, bán kính R, cung có số đo \(45^\circ \) là:
A. \(\frac{{\pi {R^2}}}{{45}}\)
B. \(\frac{{\pi {R^2}}}{4}\)
C. \(\frac{{\pi {R^2}}}{8}\)
D. \(\frac{{\pi {R^2}}}{{16}}\)
Bài 13 :
Quay lại hoạt động gấp hình tròn trong Hoạt động 1.
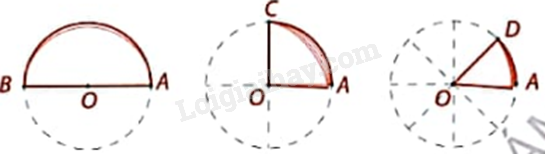
Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?

Bài 14 :
Quay lại hoạt động gấp hình tròn trong Hoạt động 1.
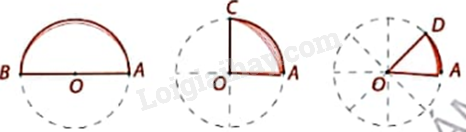
Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?

Bài 15 :
Trong Hình 5.54, chiếc quạt có dạng một hình quạt tròn tâm O cung AB, bán kính \(OA = OB = 20cm\). Giấy được dán trong phần giới hạn bởi cung AB, cung CD, đoạn thẳng AC và BD với \(OC = OD = 10cm\). Biết khi mở rộng tối đa, hai nan quạt ngoài cùng tạo thành một góc \(\widehat {AOB} = {140^o}\). Tính chu vi và diện tích mảnh giấy để dán một mặt quạt (diện tích mép không đáng kể).

Bài 16 :
Độ dài L (đơn vị cm) của cung tròn và diện tích S của hình quạt tròn (đơn vị \(c{m^2}\)) có cùng bán kính 9cm và cùng ứng với cung \({280^o}\) là:
A. \(L = 7\pi \) và \(S = 63\pi \).
B. \(L = 14\pi \) và \(S = 63\pi \).
C. \(L = 7\pi \) và \(S = 28\pi \).
D. \(L = 14\pi \) và \(S = 28\pi \).
Bài 17 :
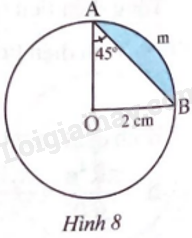
Quan sát Hình 8 và tính
a) Số đo cung AmB.
b) Độ dài cung AmB.
c) Diện tích hình quạt tròn OAmB.
d) Diện tích hình viên phân giới hạn bởi cung AmB và dây AB.
Bài 18 :
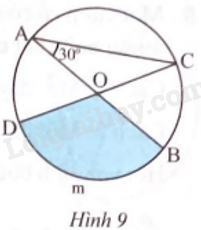
Cho đường tròn (O) đường kính AB = 3 cm, \(\widehat {CAB}\) = 30o (Hình 9).
a) Tính độ dài cung BmD.
b) Tính diện tích hình quạt tròn OBmD.
Bài 19 :
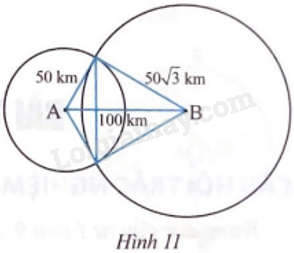
Hai trạm phát sóng A và B đặt cách nhau 100 km. Trạm phát sóng A và trạm phát sóng B có bán kính hoạt động lần lượt là 50 km và \(50\sqrt 3 \) km. Tính diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B. Biết rằng nếu khoảng cách từ thiết bị thu sóng đến trạm phát sóng lớn hơn bán kính hoạt động của trạm phát sóng thì thiết bị không thu được sóng của trạm phát sóng đó.
Bài 20 :
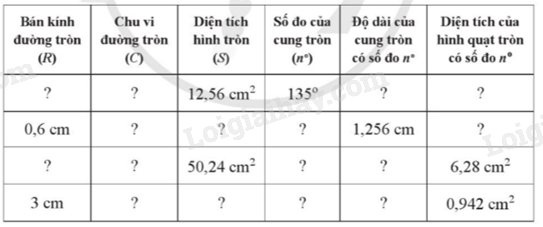
Hoàn thành số liệu ở bảng sau (làm tròn kết quả đến hàng phần trăm của đơn vị đo đã cho nếu cần, lấy \(\pi \approx 3,14\)):
Bài 21 :
Để giúp tàu hỏa chuyển từ đường ray theo hướng này sang đường ray theo hướng khác người ta làm một đoạn đường ray hình vòng cung (hình 6). Biết độ rộng của đường ray là \(AB \approx 1,1\left( m \right)\) và đoạn \(BC \approx 28,4\left( m \right)\). Hãy tính bán kính \(R = OA\) của đoạn đường ray hình vòng cung. (Tính bằng đơn vị: m, làm tròn đến hàng đơn vị).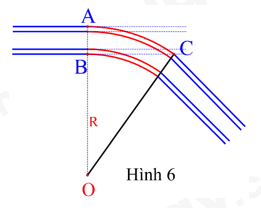


















Danh sách bình luận