An gấp đôi tờ giấy hình tròn sao cho mép của hai nửa hình tròn trùng lên nhau, sau đó tiếp tục gấp đôi để xác định trung điểm của đường gấp đầu tiên (Hình 5.6). Bạn An khẳng định rằng giao điểm của các đường gấp sau khi mở giấy chính là tâm của hình tròn ban đầu. Em hãy giải thích vì sao?
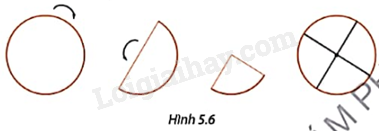
Trung điểm của đường kính là tâm của đường tròn.
Khi An gấp đôi tờ giấy hình tròn sao cho mép của hai nửa hình tròn trùng lên nhau thì đường mép gấp đó chính là đường kính của hình tròn.
Khi tiếp tục gấp đôi để xác định trung điểm của đường gấp đầu tiên, tức là ta xác định trung điểm của đường kính hình tròn. Do đó, điểm đó chính là tâm của hình tròn ban đầu.
Các bài tập cùng chuyên đề
Số tâm đối xứng của đường tròn là:
Tâm đối xứng của đường tròn là:
Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:
a) Điểm đối xứng với nó qua tâm O cũng thuộc (O).
b) Điểm đối xứng với nó qua một đường thẳng d tùy ý đi qua O cũng thuộc (O).
Trở lại tình huống mở đầu, bằng cách gấp mảnh giấy hình tròn theo hai cách khác nhau, Oanh có thể tìm được tâm của hình tròn. Em hãy làm thử xem.
Cho đường tròn \(\left( {O;R} \right)\)
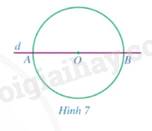
a) Vẽ đường thẳng \(d\) đi qua tâm \(O\) cắt đường tròn tại \(A,B\). So sánh \(OA\) và \(OB\) (Hình 7).
b) Giả sử \(M\) là một điểm tùy ý trên đường tròn \(\left( {O;R} \right)\). Trên tia đối của tia \(OM\), ta lấy điểm \(N\) sao cho \(ON = OM\). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
Cho đường tròn \(\left( {O;R} \right)\). Giả sử \(d\) là đường thẳng đi qua tâm \(O\) và \(M\) là một điểm tùy ý trên đường tròn \(\left( {O;R} \right)\). Kẻ \(MH \bot d\left( {H \in d} \right)\). Trên tia \(MH\) lấy điểm \(N\) sao cho \(H\) là trung điểm của \(MN\) (ta gọi điểm \(N\) là điểm đối xứng với điểm \(M\) qua đường thẳng \(d\)). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
Đường tròn có đường kính AB. Xác định tâm đối xứng của đường tròn.
Tâm đối xứng của đường tròn là
Cho Hình 5.11, trong đó tất cả các cung AB, BC, CD, DE, EG và GA đều có số đo bằng \({60^o}\). Khi đó:
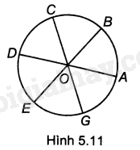
A. Điểm đối xứng với A qua CG là B.
B. Điểm đối xứng với A qua CG là D.
C. Điểm đối xứng với A qua CG là E.
D. Điểm đối xứng với A qua CG là G.
Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn (A và B là hai tiếp điểm).
a) Chứng minh rằng \(PO \bot AB\).
b) Gọi C là điểm đối xứng với A qua O. Chứng minh rằng BC//PO.
c) Tính độ dài các cạnh của tam giác PAB, biết OA=3cm và OP=5cm.
Cho một điểm A bất kì trên đường tròn (O). Xác định điểm đối xứng của A qua tâm O của đường tròn.
