Cho hàm số \(y = f\left( x \right) = x - 1 + \frac{2}{{x + 1}}\) có đồ thị (C) và đường thẳng \(y = x - 1\) như Hình 1.24.
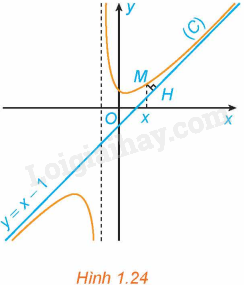
a) Với \(x > - 1\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = x - 1\). Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?
b) Chứng tỏ rằng \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = 0\). Tính chất này thể hiện trên Hình 1.24 như thế nào?
Sử dụng kiến thức về giới hạn của hàm số để tính giới hạn.
a) Nhìn vào đồ thị ta thấy, khi \(x \to + \infty \) thì khoảng cách MH tiến tới 0.
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {x - 1 + \frac{2}{{x + 1}} - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{2}{x}}}{{1 + \frac{1}{x}}} = 0\).
Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng \(y = x - 1\) tiến đến 0 khi \(x \to + \infty \).

Các bài tập cùng chuyên đề
Bài 1 :
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 2}}{{x + 2}}\) là
A. \(y = - 2\).
B. \(y = 1\).
C. \(y = x + 2\).
D. \(y = x\).
Bài 2 :
Tìm tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\).
Bài 3 :
Chứng minh rằng đường thẳng \(y = - x\) là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\).
Bài 4 :
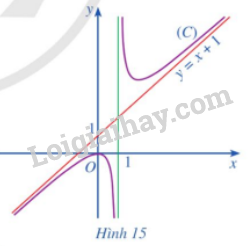
Cho hàm số \(y = f\left( x \right) = x + 1 + \frac{1}{{x - 1}}\) có đồ thị \(\left( C \right)\) và đường thẳng \(y = x + 1\) (Hình 15). Tìm \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right];\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right]\)
Bài 5 :
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 3x + 5}}{{x + 2}}\) là:
A. \(y = x\).
B. \(y = x + 1\).
C. \(y = x + 2\).
D. \(y = x + 3\).
Bài 6 :
Tìm tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 3x}}{{x + 5}}\)
Bài 7 :
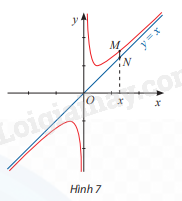
Cho đồ thị của hàm số \(y = \frac{{{x^2} + 1}}{x}\) và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7).
a) Tính \(\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x)\) và \(\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x)\)
b) Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to - \infty \)
Bài 8 :
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^3} + 3{x^2} - 3}}{{{x^2} - 1}}\) là đường thẳng có phương trình
A. \(y = 2x + 3\) B. \(y = x + 3\) C. \(y = 2x + 1\) D. \(y = x + 1\)
Bài 9 :
Cho hàm số f(x) có đồ thị như hình dưới đây:
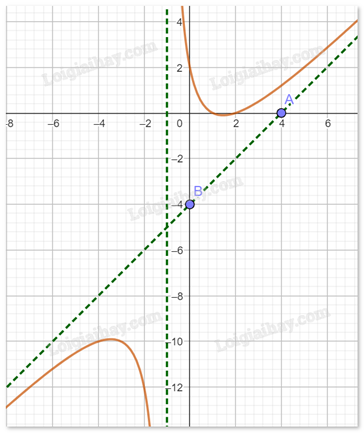
Đường tiệm cận xiên của đồ thị đã cho là đường thẳng:
-
A.
y = x - 4
-
B.
y = x + 4
-
C.
y = 4x
-
D.
y = 4
Bài 10 :
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 4x - 7}}{{x - 2}}\) là:
-
A.
y = x + 6
-
B.
y = x – 6
-
C.
y = 6x
-
D.
y = 6
Bài 11 :
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{ - {x^2} + 4x - 1}}{{x + 3}}\) là:
-
A.
y = x + 7
-
B.
y = -x + 7
-
C.
y = x - 7
-
D.
y = -x - 7
Bài 12 :
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 9x + 3}}{{x + 2}}\) là:
-
A.
y = 2x + 13
-
B.
y = -2x + 13
-
C.
y = 2x - 13
-
D.
y = -2x - 13
Bài 13 :
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 4x + 2}}{{ - 2x + 3}}\) là:
-
A.
\(y = - \frac{1}{2}x - \frac{5}{4}\)
-
B.
\(y = \frac{1}{2}x + \frac{5}{4}\)
-
C.
\(y = \frac{1}{2}x - \frac{5}{4}\)
-
D.
\(y = - \frac{1}{2}x + \frac{5}{4}\)
Bài 14 :
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 3x}}{{x - 2}}\) là:
-
A.
\(y = x - 5\)
-
B.
\(y = 5x\)
-
C.
\(y = x + 5\)
-
D.
\(y = - x - 5\)
Bài 15 :
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 1}}{x}\) là:
-
A.
\(y = x + 2\)
-
B.
\(y = - x - 2\)
-
C.
\(y = 2x\)
-
D.
\(y = 2\)
Bài 16 :
Tiệm cận xiên của đồ thị hàm số \(y = 2x - 1 - \frac{2}{{x + 1}}\) là đường thẳng:
A. \(y = 2x\).
B. \(y = x + 1\).
C. \(y = 2x - 1\).
D. \(y = - 2x + 1\).
Bài 17 :
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{3{{\rm{x}}^2} + x - 2}}{{x - 2}}\) là đường thẳng:
A. \(y = - 3{\rm{x}} + 7\)
B. \(y = 3{\rm{x}} + 7\)
C. \(y = 3{\rm{x}} - 7\)
D. \(y = - 3{\rm{x}} - 7\)
Bài 18 :
Cho hàm số \(y = \frac{{{x^2} - 2{\rm{x}} + 6}}{{x + 1}}\).
A. Đồ thị hàm số có một tiệm cận xiên là \(y = x - 3\).
B. Đồ thị hàm số có một tiệm cận xiên là \(y = x + 3\).
C. Đồ thị hàm số có một tiệm cận xiên là \(y = x + 1\).
D. Đồ thị hàm số không có tiệm cận xiên.
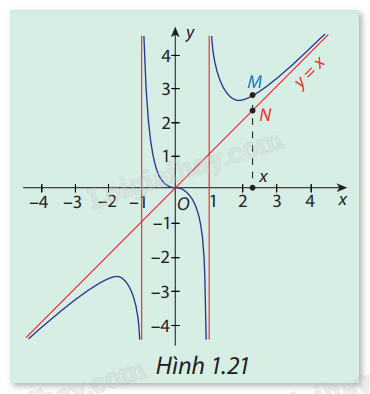
Bài 19 :
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số \(y = f(x) = x + \frac{x}{{{x^2} - 1}}\) và đường thẳng \(\Delta :y = x\) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và\(\Delta \) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi\(x \to - \infty \) và \(x \to + \infty .\)
Bài 20 :
Sử dụng ghi chú ở trên, tìm tiệm cận xiên của đồ thị hàm số \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\).
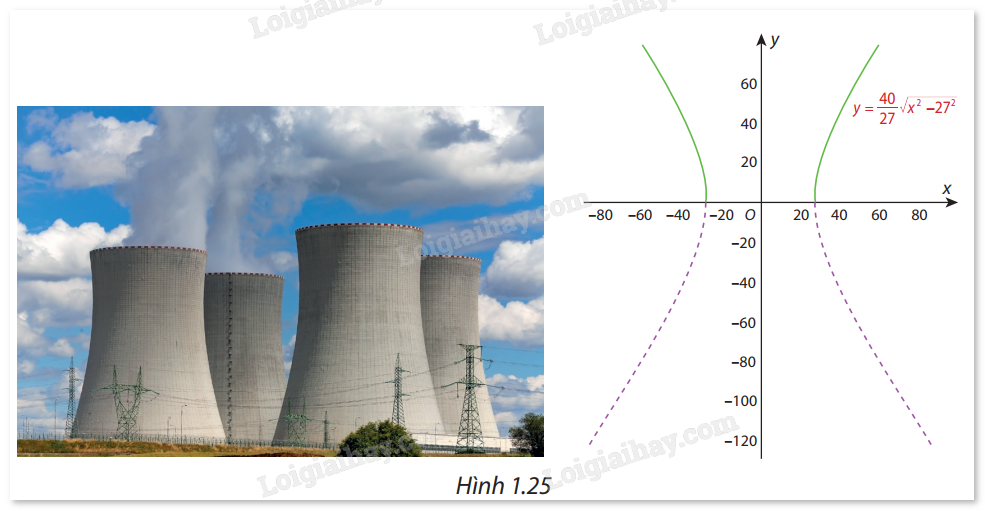
Bài 21 :
Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (Hình 1.25). Hét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số \(y = \frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} \) (phần nét liền đậm). Chứng minh rằng đường thẳng \(y = \frac{{40}}{{27}}x\) là một đường tiệm cận của (C). Hãy chỉ ra them một đường tiệm cận xiên khác của (C).
Bài 22 :
Cho hàm số \(f(x) = x + 2 - \frac{1}{{x - 1}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
-
A.
y = x - 1
-
B.
y = x + 2
-
C.
y = x + 1
-
D.
y = x – 2
Bài 23 :
Cho hàm số \(f(x) = x - 3 + \frac{5}{{x - 2}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
-
A.
y = x – 5
-
B.
y = x – 2
-
C.
y = x – 3
-
D.
y = x + 2
Bài 24 :
Cho hàm số \(f(x) = x + 1 + \frac{3}{{x - 6}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
-
A.
y = x – 5
-
B.
y = x – 1
-
C.
y = x + 1
-
D.
y = x + 6
Bài 25 :
Cho hàm số \(f(x) = x - 3 + \frac{1}{{2 - x}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
-
A.
y = 2 – x
-
B.
y = x – 2
-
C.
y = x + 3
-
D.
y = x – 3
Bài 26 :
Đồ thị của hàm số \(y = 2x + 1 + \frac{2}{{3x - 1}}\) có đường tiệm cận xiên là
-
A.
\(y = 3x - 1\)
-
B.
\(y = 2 + x\)
-
C.
\(y = 3 - x\)
-
D.
\(y = 2x + 1\)
Bài 27 :
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x + 1}}\) là:
-
A.
\(y = x + 1\)
-
B.
\(y = x - 1\)
-
C.
\(y = x - 3\)
-
D.
\(y = x + 3\)
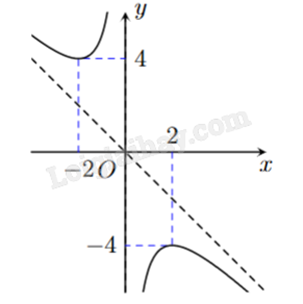
Bài 28 :
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{x}\) \((ac \ne 0)\) có đồ thị như hình vẽ. Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng
-
A.
Đường thẳng y = x
-
B.
Đường thẳng y = -x
-
C.
Đường thẳng x = 0
-
D.
Đường thẳng y = 2x
Bài 29 :
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (với \(a \ne 0\), \(m \ne 0\)) có đồ thị như hình vẽ dưới đây.
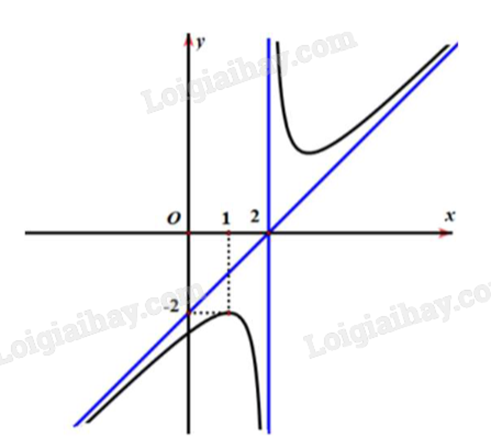
Phương trình đường tiệm cận xiên của đồ thị hàm số đã cho là
-
A.
y = 2x + 2
-
B.
y = x – 2
-
C.
y = 2x – 2
-
D.
y = x + 2
Bài 30 :
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{dx + e}}\) (với \(a,b,c,d,e \in \mathbb{R}\), \(ad \ne 0\)) có đồ thị như hình vẽ.
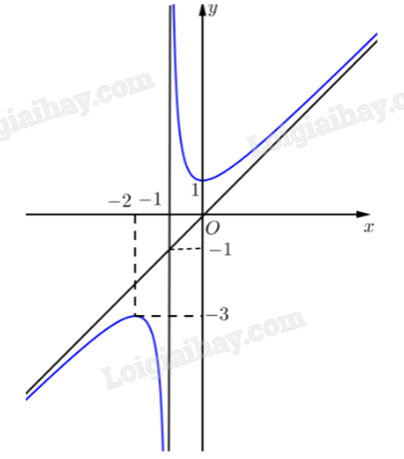
Tiệm cận xiên của đồ thị hàm số đã cho là
-
A.
\(y = - x\)
-
B.
\(y = x\)
-
C.
\(y = x - 1\)
-
D.
\(y = x + 1\)


















Danh sách bình luận