Một tam giác vuông có hiệu độ dài hai cạnh góc vuông là 7 cm. Tính diện tích của tam giác vuông đó biết nó nội tiếp trong đường tròn đường kính 13 cm.
Đường tròn ngoại tiếp tam giác vuông có bán kính bằng nửa cạnh huyền.
Bước 1: Lập phương trình:
Chọn ẩn số và đặt điều kiện cho ẩn số.
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: Kiểm tra xem nghiệm có thoả mãn điều kiện của ẩn hay không rồi kết luận.
Ta có cạnh huyền có độ dài là 2R bằng đường kính là 13 cm
Gọi cạnh góc vuông là x (x > 0)
Suy ra cạnh góc vuông còn lại x – 7 (cm)
Áp dụng định lí Pythagore vào tam giác vuông ta có:
\(\begin{array}{l}{x^2} + {\left( {x - 7} \right)^2} = {13^2}\\2{x^2} - 14x - 120 = 0\end{array}\)
Giải phương trình ta được \({x_1} = 12(TM);{x_2} = - 5(L)\)
Vậy độ dài hai cạnh góc vuông là 12 cm và 5 cm.
Suy ra diện tích tam giác vuông là: \(\frac{1}{2}.12.5 = 30\)\(c{m^2}\)
Các bài tập cùng chuyên đề
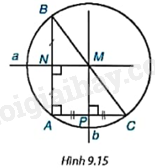
Cho tam giác ABC vuông tại đỉnh A (H.9.15). Gọi N, P lần lượt là trung điểm của các cạnh AB và AC.
a) Vẽ hai đường trung trực a, b của các cạnh AB, AC, cắt nhau tại M.
b) Hãy giải thích vì sao MN, MP là các đường trung bình của tam giác ABC.
c) Hãy giải thích vì sao M là trung điểm của BC, từ đó suy ra đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính \(MB = MC = \frac{{BC}}{2}\).
Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng tam giác ABC vuông cân tại A và có cạnh bên bằng \(2\sqrt 2 cm\).
Cho tam giác vuông cân ABC có AB = AC = 4 cm. Bán kính R của đường tròn ngoại tiếp tam giác có độ dài là
A. 2\(\sqrt 2 \) cm.
B. \(\sqrt 2 \) cm.
C. 4\(\sqrt 2 \) cm.
D. 8\(\sqrt 2 \) cm.
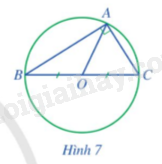
Cho tam giác ABC vuông tại A. Gọi O là trung điểm của BC (hình 7). Đường tròn (O; OB) có phải là đường tròn ngoại tiếp tam giác ABC hay không?
Nêu cách sử dụng ê ke để xác định tâm của một đường tròn bất kì khi chưa biết tâm của nó.
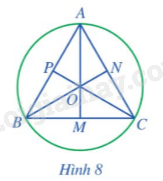
Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 8).
a) AM, BN, CP có là các đường trung trực của tam giác ABC hay không?
b) Điểm O có là tâm đường tròn ngoại tiếp tam giác ABC hay không?
c) Tính AM theo a.
d) Tính OA theo a.
Tính bán kính của đường tròn ngoại tiếp tam giác vuông có hai cạnh góc vuông lần lượt bằng 5 cm và 12 cm.
Chứng minh nếu tâm đường tròn ngoại tiếp \(\Delta \)ABC là trung điểm M của cạnh BC thì \(\Delta \)ABC vuông tại A.
Tam giác vuông ABC có hai cạnh góc vuông lần lượt bằng 6 cm và 8 cm. Diện tích đường tròn ngoại tiếp \(\Delta \)ABC bằng
A. \(10\pi \) cm2
B. 20\(\pi \) cm2
C. 25\(\pi \)cm2
D. 100\(\pi \) cm2
Bán kính của đường tròn ngoại tiếp tam giác mà độ dài ba cạnh 3cm, 4cm, 5cm là:
