Đề bài

Có bao nhiêu giá trị nguyên dương của \(n\) để \(\dfrac{9}{{4n + 1}}\) đạt giá trị nguyên.

• A. \(1\)
• B. \(0\)  
• C. \(2\)
• D. \(3\)

Phương pháp giải

Phân số \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\) là một số nguyên nếu \(b\) là ước của $a$

Lời giải của GV Loigiaihay.com

Vì \(n\) nguyên dương nên để \(\dfrac{9}{{4n + 1}}\) nguyên thì \(4n + 1 \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\)

Ta có bảng:

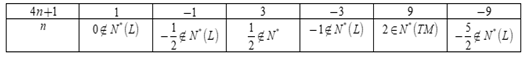
Vậy có duy nhất một giá trị của \(n\) thỏa mãn là \(n = 2\)

Đáp án : A

Chú ý

Một số em có thể sẽ chọn nhầm đáp án \(C\) vì nghĩ số \(0\) cũng là số nguyên dương hoặc \(D\) vì quên rằng \(n\) là số nguyên dương.