Có một quả bóng rổ (loại số 7 cho nam) và một quả bóng tennis (Hình 45). Biết rằng diện tích bề mặt của quả bóng rổ khoảng 1 884,75 cm2 và bán kính của quả bóng rổ gấp khoảng 2 lần đường kính của quả bóng tennis. Hỏi diện tích bề mặt của quả bóng tennis đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần mười)?
Bước 1: Tính bán kính bóng rổ dựa vào công thức tính diện tích bề mặt \(4\pi {R^2} \approx 1884,75.\)
Bước 2: Tính bán kính bóng tennis (đường kính bóng tennis = bán kính bóng rổ : 2).
Bước 3: Tính diện tích bề mặt bóng tennis.
Diện tích bề mặt bóng rổ khoảng 1 884,75 cm2 nên ta có \(4\pi {R^2} \approx 1884,75\), suy ra \(R \approx \frac{{\sqrt {7539\pi } }}{4\pi}cm.\)
Đường kính bóng tennis là khoảng:
\(\frac{{\sqrt {7539\pi } }}{4\pi}:2 = \frac{{\sqrt {7539\pi } }}{8\pi}\) (cm).
Bán kính bóng tennis là khoảng:
\(\frac{{\sqrt {7539\pi } }}{8\pi}:2 = \frac{{\sqrt {7539\pi } }}{{16\pi}}\) (cm).
Diện tích bề mặt bóng tennis là:
\(4.\pi .{\left( {\frac{{\sqrt {7539\pi } }}{{16\pi}}} \right)^2} \approx 117,8\left( {c{m^2}} \right).\)
Vậy diện tích bề mặt của quả bóng tennis khoảng \(117,8\left( {c{m^2}} \right).\)
Các bài tập cùng chuyên đề
Người ta thấy rằng lượng sơn cần dùng để sơn kín một mặt cầu bán kính R bằng với lượng sơn cần dùng để sơn kín một hình tròn bán kính 2R (khi độ dày của lớp sơn như nhau) (H.10.24). Từ đó, em hãy dự đoán công thức tính diện tích mặt cầu bán kính R.
Khinh khí cầu đầu tiên được phát minh bởi anh em nhà Montgolfler (người Pháp) vào năm 1782. Chuyến bay đầu tiên của hai anh em trên khinh khí cầu được thực hiện vào ngày 4 tháng 6 năm 1783 trên bầu trời Place des Cordeliers ở Annonay (nước Pháp) (theo cand.com.vn). Giả sử một khinh khí cầu có dạng hình cầu với đường kính bằng 11m. Tính diện tích mặt khinh khí cầu đó (làm tròn kết quả đến hàng đơn vị của \({m^2}\)).
Một quả bóng đá có chu vi của đường tròn lớn bằng 68,5cm. Quả bóng được ghép nối bởi các miếng da hình lục giác đều màu trắng và đen, mỗi miếng có diện tích bằng \(49,83c{m^2}\). Hỏi cần ít nhất bao nhiêu miếng da để làm quả bóng trên? (Coi phần mép khâu không đáng kể).
Hằng năm cứ dịp Tết đến Xuân về, dân làng Thúy Lĩnh, phường Lĩnh Nam, quận Hoàng Mai, Hà Nội lại tổ chức lễ hội vật cầu truyền thống. Trong lễ hội có sử dụng một quả cầu được tiện bằng gỗ, đường kính khoảng 35cm, sơn đỏ mặt ngoài. Tính diện tích mặt ngoài của quả cầu gỗ nói trên.
Diện tích mặt cầu có đường kính 10cm là
A. \(10\pi \;c{m^2}\).
B. \(400\pi \;c{m^2}\).
C. \(50\pi \;c{m^2}\).
D. \(100\pi \;c{m^2}\).
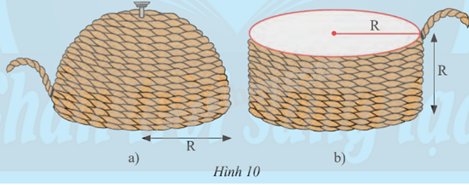
Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R.
a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b.
b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.
Tìm diện tích bề mặt của Mặt Trăng, biết đường kính Mặt Trăng là khoảng
3474 km.
Độ dài đoạn thẳng nối hai điểm bất kì trên mặt cầu bán kính 20 cm và đi qua tâm là
A. 40 m.
B. 20 cm.
C. 40 cm.
D. 80 cm.
Diện tích của mặt cầu có bán kính 5 cm là
A. 25\(\pi \)cm2.
B. 50\(\pi \)cm2.
C. 100\(\pi \)cm2.
D. 125\(\pi \)cm2.
Bạn Nam được tặng một quả bóng đá có đường kính 24 cm (Hình 2). Em hãy giúp bạn ấy tính xem cần bao nhiêu diện tích da để làm bóng, giả sử rằng diện tích các mép nối không đáng kể.
Thực hiện các hoạt động sau:
a) Chuẩn bị một mặt cầu bằng nhựa (chẳng hạn quả bóng bằng nhựa mỏng) có bán kính là R và một hình trụ bằng bìa cứng (hoặc nhựa mỏng) có bán kính đáy là R và chiều cao là 2R (như Hình 35a) một cuộn dây mảnh, không dãn (chẳng hạn dây len) đủ dài.
b) Dùng cuộn dây đó cuốn dần dần để phủ kín một nửa mặt cầu rồi cắt dây ở điểm cuối cùng (Hình 35b). Như vậy đoạn dây thứ nhất “đã lát kín” một nửa mặt cầu. Tiếp tục dùng cuộn dây đó cuốn dần dần để phủ kín mặt xung quanh của hình trụ và cắt dây ở điểm cuối cùng (Hình 35c). Ta được đoạn dây thứ hai “lát kín” mặt xung quanh của hình trụ đã cho.
Gỡ từng đoạn dây quấn quanh nửa mặt cầu và mặt xung quanh của hình trụ nói trên, ta thấy hai đoạn dây đó có độ dài bằng nhau.
Do hai đoạn dây lần lượt lát kín một nửa mặt cầu, mặt xung quanh của hình trụ và độ dài hai đoạn dây đó bằng nhau nên ta có thể coi hai mặt đó có diện tích bằng nhau.
c) Tính diện tích xung quanh của hình trụ có bán kính đáy là R và chiều cao là 2R. Từ đó, hãy nêu dự đoán về công thức tính diện tích của mặt cầu bán kính R.
Một quả bóng đá theo tiêu chuẩn chuyên nghiệp (cho cả nam và nữ, từ khoảng 11, 12 tuổi trở lên), thường nặng khoảng 450 g, có chu vi đường tròn lớn khoảng 70 cm. Diện tích bề mặt của quả bóng đá như thế bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)?
Để dự báo thời tiết, người ta sử dụng các bóng thám không, đó là một loại bóng bay mang theo các dụng cụ đo thời tiết như đo áp suất khí quyển, nhiệt độ, độ ẩm và tốc độ gió. Giả sử một quả bóng thám không có dạng hình cầu với bán kính 10 m. Hỏi diện tích bề mặt của quả bóng thám không đó là bao nhiêu mét vuông?
Trái Đất được xem như một hình cầu với bán kính khoảng 6371 km. Nếu coi xích đạo là đường tròn lớn của hình cầu này thì độ dài đường xích đạo là bao nhiêu kilomet?
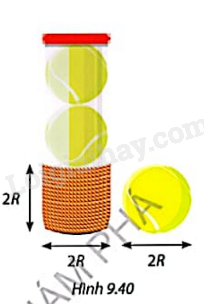
Bạn An dùng một sợi dây dù dài và mỏng cuốn quanh một quả bóng đến khi bọc kín quả bóng đó bằng các vòng cuốn sát nhau và không chồng lên nhau (Hình 9.39).
Bạn An cắt sợi dây dù tại điểm kết thúc quá trình cuốn dây quanh quả bóng, rồi lấy đoạn dây này cuốn từng vòng sát nhau quanh hộp hình trụ đựng quả bóng đó (Hình 9.40). Bạn An thấy rằng đoạn dây cuốn quanh hộp đựng bóng tạo thành một hình trụ có đường kính và chiều cao cùng bằng đường kính quả bóng.
a) So sánh diện tích bề mặt quả bóng với phần diện tích của hộp đựng bị quấn bởi sợi dây dù.
b) Gọi R là bán kính của quả bóng. Viết công thức tính diện tích xung quanh của hình trụ do đoạn dây cuốn quanh hộp đựng bóng tạo thành theo R, từ đó suy ra diện tích bề mặt của quả bóng.
Một mặt cầu có diện tích là 36 cm2. Hỏi đường kính của mặt cầu này là bao nhiêu centimet (làm tròn kết quả đến hàng phần trăm)?
Đại dương bao phủ khoảng 71% bề mặt Trái Đất. Hãy ước tính diện tích của đại dương theo kilomet vuông, biết bán kính Trái Đất khoảng 6371 km (làm tròn kết quả đến hàng triệu).
