Cầu Trường Tiền (hay Tràng Tiền) ở thành phố Huế được khởi công vào tháng 5/1899 và khánh thành vào ngày 18/12/1900. Cầu được thiết kế theo kiến trúc Gothic, bắc qua sông Hương. Từ Festival Huế năm 2002, cầu Trường Tiền được lắp đặt một hệ thống chiếu sáng đổi màu hiệ đại. Cầu dài 402,60m gồm 6 nhịp dầm thép.
Giả sử một nhịp dầm thép có dạng parabol \(y = a{x^2}\) trong hệ trục tọa độ Oxy, ở đó Ox song song với mặt cầu. Biết rằng hai chân nhịp dầm thép đến mặt cầu là 5,45 m (Hình 11).
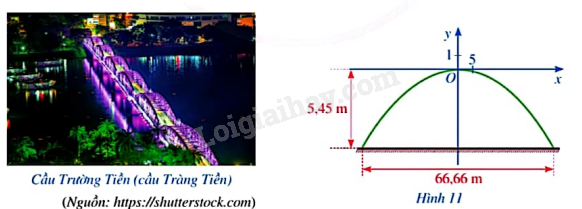
a) Xác định tọa độ của hai chân nhịp cầu trên.
b) Tìm a (làm tròn đến kết quả hàng phần nghìn).
a) Dựa vào hình và dữ kiện, xác định tung độ và hoành độ của 2 chân nhịp cầu.
b) Thay tọa độ 1 trong 2 điểm vừa tìm được vào hàm số\(y = a{x^2}\) để tìm a.
a) Gọi tọa độ của hai chân nhịp cầu là \(\left( {{x_1};{y_1}} \right),\left( {{x_2};{y_2}} \right).\)
Vì hai chân nhịp dầm thép đến mặt cầu là 5,45 m nên tung độ của 2 chân nhịp cầu là \({y_1} = {y_2} = - 5,45.\)
Độ dài của một nhịp dầm là 66,66 m nên hoành độ của 2 chân nhịp cầu là \({x_1} = - \frac{{66,66}}{2} = - 33,33;{x_2} = \frac{{66,66}}{2} = 33,33.\)
Vậy tọa độ của hai chân nhịp cầu là \(\left( { - 33,33; - 5,45} \right),\left( {33,33; - 5,45} \right).\)
b) Vì \(\left( { - 33,33; - 5,45} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\) nên ta có:
\(\begin{array}{l} - 5,45 = a{\left( {33,33} \right)^2}\\a \approx 0,005\end{array}\)
Vậy \(a \approx 0,005\).

Các bài tập cùng chuyên đề
Bài 1 :
Giải quyết bài toán ở tình huống mở đầu.
Tình huống mở đầu
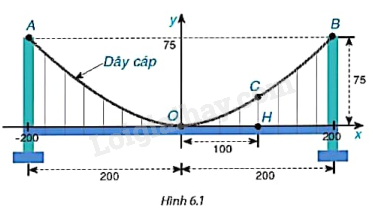
Một cây cầu treo có trụ tháp đôi cao 75m so với mặt của cây cầu và cách nhau 400m. Các dây cáp có dạng đồ thị của hàm số \(y = ax^2 (a \ne 0)\) như Hình 6.1 và được treo trên các đỉnh tháp. Tính chiều cao CH của dây cáp biết điểm H cách tâm O của cây cầu 100m (giả sử mặt của cây cầu là bằng phẳng).
Bài 2 :
Cho hình lăng trụ đứng có đáy là hình vuông cạnh a (cm) và chiều cao 10cm.
a) Viết công thức tính thể tích V của lăng trụ theo a và tính giá trị của V khi \(a = 2cm\).
b) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của lăng trụ thay đổi thế nào?
Bài 3 :
Diện tích toàn phần \(S\left( {c{m^2}} \right)\) của hình lập phương, tức là tổng diện tích xung quanh và diện tích đáy hai mặt của hai mặt đáy là một hàm số của độ dài cạnh a (cm).
a) Viết công thức của hàm số này.
b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là \(54c{m^2}\).
Bài 4 :
Một cổng vòm được thiết kế dạng parabol \(y = a{x^2}\) như Hình 6.8. Biết chiều rộng của chân cổng là \(AB = 6m\) và chiều cao của cổng là \(OI = 4,5m\).
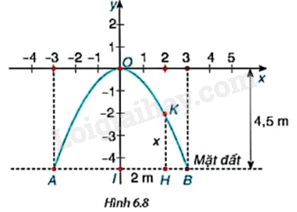
a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2m.
b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2m, chiều cao 3m. Hỏi xe tải này có thể đi qua được cổng vòm hay không?
Bài 5 :
Cho hàm số \(y = a{x^2}\). Xác định hệ số a, biết đồ thị hàm số đi qua điểm A(3; 3). Vẽ đồ thị của hàm số trong trường hợp đó.
Bài 6 :
Một vật rơi tự do từ độ cao 125 m so với mặt đất. Quãng đường chuyển động s (m) của vật phụ thuộc và thời gian t (giây) được cho bởi công thức s = 5t2 .
a) Sau 2 (giây), vật này cách mặt đất bao nhiêu mét? Tương tự, sau 3 giây vật này cách mặt đất bao nhiêu mét?
b) Sau bao lâu thì vật này tiếp đất?
Bài 7 :
Động năng (tính bằng J) của một quả bưởi nặng 1 kg rơi với tốc độ v (m/s) được tính bằng công thức \(K = \frac{1}{2}{v^2}\).
a) Tính động năng của quả bưởi đạt được khi nó rơi với tốc độ lần lượt là 3 m/s, 4 m/s.
b) Tính tốc độ rơi của quả bưởi tại thời điểm quả bưởi đạt được động năng 32 J.
Bài 8 :
Cho hàm số y = - x2.
a) Lập bảng giá trị của hàm số.
b) Vẽ đồ thị hàm số.
Bài 9 :
Cho hàm số y = \(\frac{1}{2}\)x2.
a) Vẽ đồ thị hàm số.
b) Trong các điểm A(-6;-8), B(6;8), C \(\left( {\frac{2}{3};\frac{2}{9}} \right)\), điểm nào thuộc đồ thị của hàm số trên?
Bài 10 :
Cho một hình lập phương có độ dài cạnh là x (cm).
a) Viết công thức tính diện tích toàn phần S (cm2) của hình lập phương theo x.
b) Lập bảng giá trị của hàm số S khi x lần lượt nhận các giá trị: \(\frac{1}{2}\); 1; \(\frac{2}{3}\); 2; 3.
c) Tính độ dài cạnh của hình lập phương, biết S = 54 cm2.
Bài 11 :
Khi gió thổi vuông góc vào cánh buồm của một con thuyền thì lực F(N) của nó tỉ lệ thuận với bình phương tốc độ v (m/s) của gió, tức là F = av2 (a là hằng số). Biết rằng khi tốc độ của gió bằng 3 m/s thì lực tác động lên cánh buồm bằng 180 N.
a) Tính hằng số a.
b) Với a vừa tìm được, tính lực F khi v = 15 m/s và khi v = 26 m/s.
c) Biết rằng cánh buồm chỉ có thể chịu được một lực tối đa là 14580 N, hỏi con thuyền có thể đi được trong gió bão với tốc độ gió 90 km/h hay không?
Bài 12 :
Cho hàm số \(y = \frac{1}{3}{x^2}\).
a) Tìm giá trị của y tương ứng với giái trị của x trong bảng sau:

b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số đó.
c) Tìm những điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng -6; 10.
d) Tìm những điểm thuộc đồ thị của hàm số có tung độ bằng 27.
Bài 13 :
Trên mặt phẳng tọa độ Oxy, điểm M(2;-1) thuộc đồ thị hàm số \(y = a{x^2}\).
a) Tìm hệ số a.
b) Điểm A(4;-4) có thuộc đồ thị hàm số hay không?
c) Hãy tìm một số điểm (không kể điểm O) thuộc đồ thị hàm số, rồi vẽ đồ thị của hàm số.
Bài 14 :
Cho hàm số \(y = a{t^2}\) biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125m sau khoảng thời gian là 5 giây.
a) Tìm hệ số a.
b) Vẽ đồ thị của hàm số.
Bài 15 :
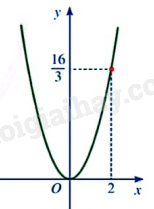
Trên mặt phẳng tọa độ Oxy, đường parabol ở Hình 10 biểu diễn đồ thị của hàm số \(y = a{x^2}\).
a) Tìm hệ số a.
b) Tìm điểm thuộc đồ thị hàm số có hoành độ bằng 3.
c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 4.
Bài 16 :
Tìm các giá trị tương ứng của hai hàm số y = 2x2 , y = - 3x2 trong Bảng 6.5 và vẽ đồ thị của mỗi hàm số.

Bài 17 :
Khối lượng tối da L (tấn) mà một loại dây có thể chịu được phụ thuộc vào đường kính d (inch) của dây theo hàm số L = ad2 (1 inch \( \approx \) 2,54 cm).
a) Tìm hệ số a, biết sợi dây có đường kính 1,5 inch chịu được khối lượng tối đa 18 tấn.
b) Một sợi dây có đường kính 26 mm sẽ chịu được khối lượng tối đa bao nhiêu tấn (làm tròn kết quả đến hàng phần trăm)?
Bài 18 :
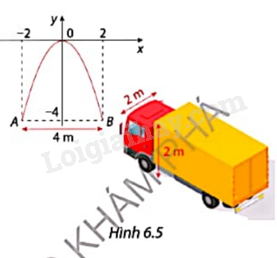
Cổng của một hội chợ được thiết kế theo hình parabol là một phần của đồ thị hàm số y = -x2. Khoảng cách giữa hai chân cổng là 4 m (Hình 6.5). Hỏi một chiếc xe tải có chiều rộng 2 m vào cao 2 m có thể đi qua cổng được không?
Bài 19 :
Cho hàm số y = ax2.
a) Tìm a, biết đồ thị hàm số đi qua điểm M(-4;8).
b) Tìm trên đồ thị hàm số điểm D có hoành độ x = -2.
Bài 20 :
Chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Cho hàm số y = ax2 (\(a \ne 0)\)
a) Giá trị a để đồ thị của hàm số đi qua điểm (2; 2) là a = 2.
b) Nếu a > 0 thì đồ thị của hàm số nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
c) Nếu a < 0 thì đồ thị của hàm số nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
d) Đồ thị của hàm số là một đường cong parabol đỉnh O, nhận trục tung làm trục đối xứng.
Bài 21 :
Cho hai hàm số \(y = \frac{3}{4}{x^2}\) và \(y = - \frac{3}{4}{x^2}\).
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng toạ độ.
b) Nhận xét về tính đối xứng của hai đồ thị qua trục Ox.
c) Xác định m để đường thẳng d: y = (3m – 2)x + 5 cắt parabol (P): \(y = \frac{3}{4}{x^2}\) tại điểm E có hoành độ bằng – 2.
Bài 22 :
Cho hình lăng trụ đứng có đáy là hình vuông cạnh \(a\left( {cm} \right)\) và chiều cao \(h = 15\left( {cm} \right)\).
a) Công thức tính thể tích \(V\) của lăng trụ theo \(a\) là \(V = 15{a^2}\).
b) Công thức \(V = 15{a^2}\) là hàm số bậc hai có đồ thị đi qua gốc tọa độ.
c) Nếu độ dài cạnh hình vuông \(a = 2\left( {cm} \right)\) thì thể tích của lăng trụ \(V = 60\left( {c{m^3}} \right)\).
d) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích hình lăng trụ tăng lên hai lần.
Bài 23 :
Công thức \(E = \frac{1}{2}m{v^2}\)(J) được dùng để tính động năng của 1 vật có khối lượng \(m\) (kg) khi chuyển động với vận tốc \(v\) (m/s).
a) Công thức tính động năng của vật là hàm số bậc hai.
b) Đồ thị hàm số \(y = \frac{1}{2}m{v^2}\) nằm phía trên trục hoành.
c) Giả sử có một quả bóng có khối lượng \(1,5\)kg thì công thức tính động năng của vật là \(\frac{3}{2}{v^2}\).
d) Giả sử có 1 quả bóng có khối lượng \(1,5\) kg đang bay với vận tốc \(8\) m/s thì động năng của quả bóng đó là \({\rm{48 J}}\).
Bài 24 :
Cho hàm số \(y = f\left( x \right) = 0,5{x^2}\left( P \right)\) và hàm số \(y = g\left( x \right) = - 0,5{x^2}\left( {P'} \right)\).
a) Đồ thị của hai hàm số \(\left( P \right)\) và hàm số \(\left( {P'} \right)\) đều nhận Oy làm trục đối xứng.
b) Gốc \(O\left( {0;0} \right)\) là điểm chung của hai đồ thị \(\left( P \right)\) và \(\left( {P'} \right)\).
c) Điểm \(A\left( { - 2;2} \right)\) thuộc \(\left( P \right)\) nhưng không thuộc \(\left( {P'} \right)\).
d) \(2f\left( { - 30} \right) + g(10) < 0\).
Bài 25 :
Cho biết đồ thị hàm số \(y = \left( {m + 2} \right){x^2}\left( {m \ne - 2} \right)\) đi qua điểm \(A\left( { - 1; - 2} \right)\).
a) Tính giá trị của hàm số tại \(x = 3\).
b) Điểm \(B\left( {0,5; - 0,25} \right)\) có thuộc đồ thị hàm số hay không?
c) Tìm một số điểm thuộc đồ thị hàm số (khác điểm O) rồi vẽ đồ thị hàm số đó.
Bài 26 :
Người ta muốn dựng một khung cổng hình vuông ABCD có độ dài cạnh bằng 3cm được bao bởi một khung thép có dạng nửa đường tròn tâm \(F\) bán kính FA (như hình 3)
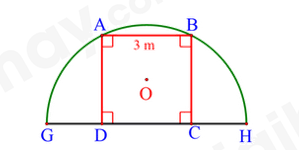
a) Độ dài đoạn thẳng của OA là \(1,5\sqrt 2 m\)
b) Độ dài đoạn thẳng \(HG = 3\sqrt 5 m\)
c) Độ dài cung GAH là \(3\sqrt 5 \pi {\mkern 1mu} {\mkern 1mu} m\)
d) Người ta muốn sơn toàn bộ nửa hình tròn (không sơn phần cổng ABCD). Giá tiền sơn 30000 đồng/m2. Biết \(\pi {\rm{\;}} = 3,14\), kết quả làm tròn đến nghìn đồng. Số tiền sơn là 1059 (nghìn đồng)
Bài 27 :
Cho hàm số \(y = \frac{{{x^2}}}{2}\)a) Vẽ đồ thị (P) của hàm số trên.
b) Tìm những điểm M thuộc (P) có tung độ và hoành độ bằng nhau.
Bài 28 :
Cho hàm số \(y = - \frac{{{x^2}}}{2}\)a) Vẽ đồ thị (P) của hàm số trên.
b) Tìm các điểm thuộc đồ thị (P) có tung độ bằng một nửa hoành độ và khác (0;0).
Bài 29 :
Cho hàm số \(\left( P \right):y = - \frac{{{x^2}}}{4}\).a) Vẽ đồ thị \(\left( P \right)\) của hàm số trên.
b) Tìm trên \(\left( P \right)\) những điểm có tung độ gấp \(3\) lần hoành độ.
Bài 30 :
Cho hàm số \(\left( P \right):y = \frac{1}{2}{x^2}\).a) Vẽ đồ thị \(\left( P \right)\) của hàm số trên.
b) Minh đang thiết kế một mô hình Parabol để mô phỏng quỹ đạo của một quả bóng trong trò chơi của mình. Quỹ đạo được biểu diễn bằng hàm số sau: \(y = \frac{1}{2}{x^2}\). Minh muốn tìm các vị trí trên quỹ đạo mà độ cao của quả bóng so với mặt đất là 0,5 mét. Hỏi tại những điểm nào trên mặt phẳng, quả bóng đạt được độ cao này?


















Danh sách bình luận