Tính giá trị của mỗi căn thức bậc ba sau:
a. \(\sqrt[3]{{2x - 7}}\) tại \(x = - 10;x = 7,5;x = - 0,5\)
b. \(\sqrt[3]{{{x^2} + 4}}\) tại \(x = 0;x = 2;x = \sqrt[{}]{{23}}\).
Thay giá trị vào biểu thức để tính.
a. Thay \(x = - 10\) vào biểu thức, ta được: \(\sqrt[3]{{2.\left( { - 10} \right) - 7}} = \sqrt[3]{{ - 20 - 7}} = \sqrt[3]{{ - 27}} = - 3\).
Thay \(x = 7,5\) vào biểu thức, ta được: \(\sqrt[3]{{2.7,5 - 7}} = \sqrt[3]{{15 - 7}} = \sqrt[3]{8} = 2\).
Thay \(x = - 0,5\) vào biểu thức, ta được: \(\sqrt[3]{{2.\left( { - 0,5} \right) - 7}} = \sqrt[3]{{ - 1 - 7}} = \sqrt[3]{{ - 8}} = - 2\).
b. Thay \(x = 0\) vào biểu thức, ta được: \(\sqrt[3]{{{0^2} + 4}} = \sqrt[3]{4}\).
Thay \(x = 2\) vào biểu thức, ta được: \(\sqrt[3]{{{2^2} + 4}} = \sqrt[3]{{4 + 4}} = \sqrt[3]{8} = 2\).
Thay \(x = \sqrt[{}]{{23}}\) vào biểu thức, ta được: \(\sqrt[3]{{{{\left( {\sqrt[{}]{{23}}} \right)}^2} + 4}} = \sqrt[3]{{23 + 4}} = \sqrt[3]{{27}} = 3\).

Các bài tập cùng chuyên đề
Bài 1 :
a) Tính giá trị của căn thức \(\sqrt[3]{{5x - 1}}\) tại \(x = 0\) và tại \(x = - 1,4.\)
b) Rút gọn biểu thức \(\sqrt[3]{{{x^3} - 3{x^2} + 3x - 1}}.\)
Bài 2 :
Rút gọn rồi tính giá trị của biểu thức \(\sqrt[3]{{27{x^3} - 27{x^2} + 9x - 1}}\) tại \(x = 7.\)
Bài 3 :
Ông An có một bể kính hình lập phương như Hình 2.
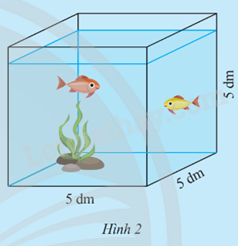
Ông An muốn làm thêm một bể kính mới hình lập phương có thể tích gấp n lần thể tích của bể kính cũ (bỏ qua bề dày của kính).
a) Gọi a (dm) là độ dài cạnh của bể kính mới. Thay mỗi ? bằng biểu thức thích hợp để nhận được các đẳng thức:
a3 = ? hay a = ?.
b) Tính giá trị của a khi n = 8 và khi n = 4 (kết quả làm tròn đến chữ số thập phân thứ hai).
Bài 4 :
Cho biểu thức Q = \(\sqrt[3]{{3{x^2}}}\). Tính giá trị của Q khi x = 2 và khi x = - 3 (kết quả làm tròn đến chữ số thập phân thứ hai).
Bài 5 :
Tính giá trị của các biểu thức:
a) A = \(\sqrt[3]{{{8^3}}} + {\left( {\sqrt[3]{{ - 7}}} \right)^3}\)
b) B = \(\sqrt[3]{{1000000}} - \sqrt[3]{{0,027}}\)
Bài 6 :
Tính giá trị của biểu thức P = \(\sqrt[3]{{64n}}\) khi n = 1; n = - 1; n = \(\frac{1}{{125}}\).
Bài 7 :
Chiều cao ngang vai của một con voi đực ở châu Phi là h (cm) có thể được tính xấp xỉ bằng công thức: \(h = 62,5.\sqrt[3]{t} + 75,8\) với t là tuổi của con voi tính theo năm.
a. Một con voi đực 8 tuổi có chiều cao ngang vai là bao nhiêu centimét?
b. Nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó bao nhiêu tuổi (làm tròn kết quả đến hàng đơn vị)?
Bài 8 :
Một cửa hàng nhận thấy rằng nếu giảm giá bán P% trong t giờ thì số khách hàng tham gia mua hàng giảm giá trong t giờ đó, gọi là N, có thể được ước tính bởi biểu thức \(N = 125\sqrt[3]{{Pt}}\). Hãy ước tính số lượng khách hàng tham gia mua hàng giảm giá 50% trong 8 giờ (làm tròn kết quả đến hàng đơn vị).
Bài 9 :
Khoảng cách trung bình d(m) giữa một hành tinh và Mặt Trời liên hệ với chu kì quỹ đạo T(s) của hành tinh (thời gian hành tinh quay một vòng quanh Mặt Trời) theo công thức \({d^3} = \frac{{{{10}^{19}}}}{{2,97}}{T^2}\) (nguồn: https://www.physicsclassroom.com/class/circles/Lesson-4/Kepler-s-Three-Laws).
a) Viết biểu thức tính d theo T.
b) Tính khoảng cách trung bình giữa Sao Hỏa và Mặt Trời theo kilômét, biết rằng chu kì quỹ đạo của Sao Hỏa là \(5,{93.10^7}\) giây (làm tròn kết quả đến hàng trăm nghìn).
Bài 10 :
Biểu thức \(\sqrt[3]{{a + 2}} + \sqrt[3]{{6a - 9}}\) có giá trị bằng 5 khi
A. \(a = - 1\).
B. \(a = 6\).
C. \(a = - 6\).
D. \(a = 1\).
Bài 11 :
Giá trị của căn thức bậc ba \(\sqrt[3]{{4x + 7}}\) tại \(x = - 2\) là:
-
A.
-1.
-
B.
0.
-
C.
1.
-
D.
Không có giá trị thỏa mãn.
Bài 12 :
Định luật Kepler về sự chuyển động của các hành tinh trong Hệ mặt trời xác định mối quan hệ giữa chu kỳ quay quanh Mặt Trời của một hành tinh và khoảng cách giữa hành tinh đó với Mặt Trời. Định luật được cho bởi công thức \({\rm{d}} = \sqrt[{\rm{3}}]{{{\rm{6}}{{\rm{t}}^{\rm{2}}}}}\). Trong đó, d là khoảng cách giữa hành tinh quay xung quanh Mặt Trời và Mặt Trời (đơn vị: triệu dặm, 1 dặm = 1609 mét), t là thời gian hành tinh quay quanh Mặt Trời đúng một vòng (đơn vị: ngày của Trái Đất).

Một năm Sao Hỏa dài bằng 687 ngày trên Trái Đất, nghĩa là Sao Hỏa quay xung quanh Mặt Trời đúng một vòng với thời gian bằng 687 ngày Trái Đất. Hãy tính khoảng cách giữa Sao Hỏa và Mặt Trời theo km. (làm tròn đến hàng phần trăm)
-
A.
140,24 triệu dặm.
-
B.
141,48 triệu dặm.
-
C.
254,83 triệu dặm.
-
D.
257,08 triệu dặm.
Bài 13 :
Rút gọn và tính giá trị của biểu thức \(\sqrt[3]{{27{x^3} - 27{x^2} + 9x - 1}}\) tại \(x = 7\).


















Danh sách bình luận