Phần bên trong của một cái bể hình trụ có chiều cao 2,1 m và bán kính đáy 1,5 m. Tính thể tích lượng nước trong bể biết mực nước bằng \(\frac{2}{3}\)chiều cao của bể (kết quả làm tròn đến hàng đơn vị).
Dựa vào công thức tính thể tích của hình trụ: V = S.h = \(\pi \)r2h
Thể tích của bể là: V = \(\pi \)r2h = \(\pi \).1,52.2,1 = 4,725\(\pi \) (m3).
Thể tích lượng nước trong bể là:
\(V' = \frac{2}{3}V = \frac{2}{3}.4,725\pi \approx\) 10 (m3).

Các bài tập cùng chuyên đề
Bài 1 :
Hãy nhắc lại công thức tính thể tích của hình lăng trụ đứng tam giác (hoặc hình lăng trụ đứng tứ giác) có diện tích đáy S và chiều cao h.
Bài 2 :
Một vòng bi bằng thép có hình dạng (phần thép giữa hai hình trụ) và kích thước như Hình 10.30. Tính thể tích của vòng bi đó.

Bài 3 :
Bạn Khôi cho một hòn đá cảnh vào một bể nuôi cá hình trụ có đường kính đáy bằng 20cm thì nước trong bể dâng lên 3cm. Hỏi hòn đá cảnh đó có thể tích bằng bao nhiêu?
Bài 4 :
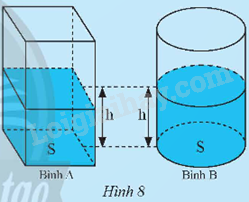
Cho hai cái bình có cùng diện tích đáy: bình A có dạng hình hộp chữ nhật, hình B có dạng hình trụ. Ban đầu cả hai bình đều không chứa nước. Người ta đổ cùng một lượng nước vào hai bình thì thấy chiều cao của mực nước hai bình bằng nhau (Hình 8). Gọi S là diện tích đáy và h là chiều cao của mực nước mỗi bình.
a) Tính thể tích V của lượng nước trong bình A theo S và h. Từ đó, dự đoán thể tích của lượng nước trong bình B.
b) Gọi r là bán kính đáy hình B. Hãy tính thể tích nước trong bình B theo r và h.
Bài 5 :
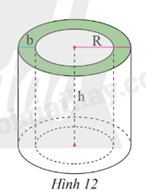
Một bể nước hình trụ có bán kính R = 1,2 m (tính từ tâm bể đến mép ngoài), bề dày của thành bể là b = 0,05 m, chiều cao lòng bể là h = 1,6 m (Hình 12). Tính dung tích của bế nước (kết quả làm tròn đến hàng phần trăm).
Bài 6 :
Thể tích của hình trụ có bán kính đáy 6 cm, chiều cao 10 cm là
A. 360\(\pi \)cm3.
B. 600\(\pi \)cm3.
C. 720\(\pi \)cm3.
D. 1200\(\pi \)cm3.
Bài 7 :
a) Nêu công thức tính thể tích hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ (Hình 7) khi biết diện tích đáy và chiều cao.
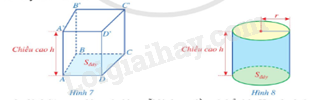
b) Cũng như hình lăng trụ đứng tứ giác, mỗi hình trụ đều có thể tích. Hãy dự đoán cách tính thể tích của hình trụ (Hình 8).
Bài 8 :
Một đường ống nối hai bể cá trong một thuỷ cung có dạng hình trụ (không có hai đáy), với độ dài (hay chiều cao) là 30 m và có dung tích là 1 800 000 lít (Hình 14). Hỏi đường kính đáy của đường ống đó là bao nhiêu mét làm tròn kết quả đến hàng phần trăm)?

Bài 9 :
Trong một thí nghiệm, bạn Mai thả một khối sắt hình trụ có chiều cao h = 6,5 cm, bán kính đáy r = 3,5 cm vào một bình chia độ đang chứa 500 ml nước. Sau khi khối sắt chìm hẳn xuống, bạn Mai thấy mực nước trong bình tăng lên vạch 750ml. Biết 1 ml = 1 cm3.

a) Dựa vào mực nước tăng lên trong bình, hãy tính thể tích của khối sắt.
b) Gọi S là diện tích đáy của khối sắt. So sánh tích S.h với kết quả ở câu a và rút ra nhận xét.
Bài 10 :
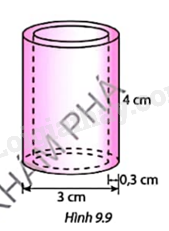
Tính thể tích nhựa cần dùng để sản xuất đoạn ống nhựa có kích thức như Hình 9.9.
Bài 11 :
Từ một tấm bìa hình chữ nhật với đồ dài hai cạnh là 20 cm, 15 cm có thể cuộn lại và dùng băng dính dán thành hình trụ A hoặc hình trụ B (không có nắp) như Hình 9.13.
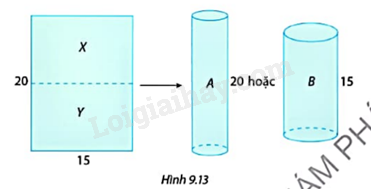
a) Hãy so sánh thể tích của hai hình trụ A và B. Giải thích câu trả lời của em.
b) Nếu cắt tấm bìa thành hai phần X, Y bằng nhau và tạo thành hai hình trụ (không có nắp) cùng chiều cao 15 cm thì tổng thể tích của hai hình trụ này có lớn hơn thể tích của hình trụ B không? Vì sao?
Bài 12 :
Một cái thớt gỗ hình trụ có đường kính đáy 40 cm, dày 5 cm như Hình 9.14.
a) Tính thể tích gỗ cần dùng để làm thớt.
b) Khối lượng riêng của gỗ làm thớt là D = 500 kg/m3. Hỏi cái thớt nặng bao nhiêu gam (làm tròn đến hàng phần mười), biết khối lượng m (kg) của một vật có thể tích V (m3) là m = D.V?

Bài 13 :
Người ta xếp 6 lon nước ngọt vừa khít trong một thùng carton có dạng hình hộp chữ nhật như Hình 9.51. Mỗi lon nước ngọt có thể xem là một hình trụ với đường kính 6,4 cm và cao 12 cm.
a) Tính tổng thể tích của 6 lon nước ngọt.
b) Các lon nước ngọt chiếm khoảng bao nhiêu phần trăm không gian trong thùng (làm tròn kết quả đến hàng phần mười)?

Bài 14 :
Tính thể tích V của hình trụ có bán kính đáy \(r = 10cm\) và chiều cao h = 30cm.
-
A.
\(V = 1000\pi \left( {c{m^3}} \right)\).
-
B.
\(V = 3000\pi \left( {c{m^3}} \right)\).
-
C.
\(V = 600\pi \left( {c{m^3}} \right)\).
-
D.
\(V = 1200\pi \left( {c{m^3}} \right)\).
Bài 15 :
Hình chữ nhật ABCD có \(AB = 3\,\left( {{cm}} \right)\), \(AD = 5\,\left( {{cm}} \right)\). Thể tích khối trụ hình thành được khi quay hình chữ nhật ABCD quanh đoạn \(AB\) bằng
-
A.
\(25\pi \,\left( {c{m^3}} \right)\).
-
B.
\(75\pi \,\left( {c{m^3}} \right)\).
-
C.
\(50\pi \,\left( {c{m^3}} \right)\).
-
D.
\(45\pi \,\left( {c{m^3}} \right)\).
Bài 16 :
Thủy cung Times City tọa lạc tại số 458 đường Minh Khai phường Vĩnh Tuy, quận Hai Bà Trưng, Hà Nội là thủy cung lớn nhất Việt Nam. Có chứa hơn 3 triệu khối nước biển với hơn ba mươi ngàn loài sinh vật biển từ khắp nơi trên thế giới. Một loại vật liệu quan trọng làm nên bể cá khổng lồ đó là tấm Acrylic – có khả năng chịu lực và chịu biến dạng tốt hơn các loại kính thông thường, kết cấu nhẹ, dẻo dai. Thể tích không khí chứa trong một đoạn ống Acrylic hình trụ có chiều dài ống 13m, đường kính đáy ngoài là 3,5 m độ dày lớp Acrylic là 500 mm khoảng
-
A.
\(63,8\left( {{m^3}} \right)\).
-
B.
\(53,8\left( {{m^3}} \right)\).
-
C.
\(43,8\left( {{m^3}} \right)\).
-
D.
\(23,8\left( {{m^3}} \right)\).
Bài 17 :
Một hộp sữa hình trụ có đường kính đáy là 13 cm. Biết diện tích vỏ hộp (kể cả nắp) là 292,5\(\pi \) \(\left( {c{m^2}} \right)\). Thể tích của hộp sữa đó là:
-
A.
\(900\pi \,\left( {{c}{{m}^3}} \right)\).
-
B.
\(676\,\left( {{c}{{m}^3}} \right)\).
-
C.
\(600\pi \,\left( {{c}{{m}^3}} \right)\).
-
D.
\(676\pi \,\left( {{c}{{m}^3}} \right)\).
Bài 18 :
Một thùng nước hình trụ có đường kính là 30cm và chiều cao là 50cm. Cần lấy khoảng bao nhiêu thùng nước như vậy để đổ đầy một bể nước có thể tích bằng 1400l (lấy \(\pi \approx 3,14\)).
-
A.
30 (thùng).
-
B.
35 (thùng).
-
C.
40 (thùng).
-
D.
25 (thùng).
Bài 19 :
Một hình trụ bán kính đường tròn đáy bằng \(1,5\,cm\) và chiều cao bằng \(4\,cm\). Người ta khoan xuyên qua hai mặt đáy của vật thể đó theo phương vuông góc với mặt đáy, phần bị khoan là một lỗ hình trụ có bán kính đường tròn đáy bằng \(0,5\,cm\). Tính thể tích phần còn lại của hình trụ đó. (lấy \(\pi \approx 3,14\) và kết quả làm tròn đến hàng đơn vị).
Bài 20 :
Một chậu hình trụ cao \(20\,{\rm{cm}}\). Diện tích đáy bằng nửa diện tích xung quanh, trong chậu có nước cao đến \(15\,{\rm{cm}}\). Hỏi phải thêm bao nhiêu nước vào chậu để nước vừa đầy chậu? (lấy \(\pi \approx 3,14\) và kết quả làm tròn đến hàng đơn vị).
Bài 21 :
Thể tích của một lon sữa hình trụ có bán kính đáy 6cm và chiều cao 10cm là
-
A.
\(360\pi c{m^3}\).
-
B.
\(600\pi c{m^3}\).
-
C.
\(720\pi c{m^3}\).
-
D.
\(1200\pi c{m^3}\).
Bài 22 :
Cho hình trụ có bán kính đáy \(R\), chiều cao \(h\). Thể tích \(V\) của hình trụ được tính bởi công thức:-
A.
\(V = \pi {R^2}h\)
-
B.
\(V = \frac{1}{3}\pi {R^2}h\)
-
C.
\(V = 2\pi Rh\)
-
D.
\(V = \pi Rh\)
Bài 23 :
Một hình trụ có bán kính đáy bằng 6cm, chiều cao bằng 10cm. Thể tích của hình trụ này là
A. \(V = 300\pi \left( {c{m^3}} \right)\).
B. \(V = 320\pi \left( {c{m^3}} \right)\).
C. \(V = 340\pi \left( {c{m^3}} \right)\).
D. \(V = 360\pi \left( {c{m^3}} \right)\).
Bài 24 :
Một hình trụ có chu vi của đường tròn đáy bằng \(4\pi a\), chiều cao bằng a. Thể tích của hình trụ này là
A. \(V = 2\pi {a^3}\).
B. \(V = 4\pi {a^3}\).
C. \(V = 16\pi {a^3}\).
D. \(V = \frac{4}{3}\pi {a^3}\).
Bài 25 :
Hình trụ có bán kính đáy bằng \(2\sqrt 3 cm\) và thể tích bằng \(24\pi \;c{m^3}\). Chiều cao của hình trụ này là
A. \(h = 2cm\).
B. \(h = 6cm\).
C. \(h = 2\sqrt 3 cm\).
D. \(h = 1cm\).
Bài 26 :
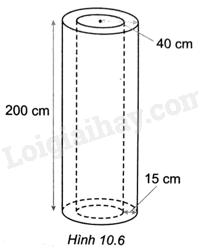
Người ta cần làm một ống thoát nước hình trụ bằng bê tông (H.10.6) có chiều cao là 200cm, độ dày của thành ống là 15cm, đường kính của ống là 80cm. Tính lượng bê tông cần dùng để làm ống thoát nước nói trên.
Bài 27 :
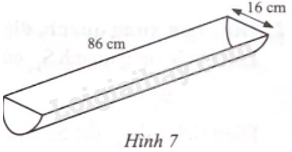
Phần bên trong của một máng nước có dạng nửa hình trụ với đường kính đáy 16 cm, chiều cao 86 cm (Hình 7). Tính dung tích của máng nước (kết quả làm tròn đến hàng đơn vị của lít).
Bài 28 :
Một ống kim loại dạng hình trụ có chiều dài 35 cm, đường kính đáy bên trong và bên ngoài của ống lần lượt là 20 mm và 28 mm (Hình 8). Tính thể tích của phần kim loại sử dụng để làm ống (kết quả làm tròn đến hàng đơn vị xăngtimet khối).

Bài 29 :
Cho hai hình trụ có bán kính đáy bằng nhau, chiều cao của hình trụ thứ nhất gấp đôi chiều cao của hình trụ thứ hai. Tỉ số thể tích của hình trụ thứ nhất và thứ hai là
A. 1:1
B. 1:2
C. 2:1
D. 3:1
Bài 30 :
Cho một hình trụ có diện tích xung quanh là \(50\pi \) cm2 và bán kính đáy là 5 cm. Thể tích của hình trụ đó là
A. \(25\pi \) cm3
B. \(125\) cm3
C. \(125\pi \) cm3
D. \(100\pi \) cm3


















Danh sách bình luận