Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Lần lượt vẽ đường tròn (O) đường kính BH và đường tròn (O’) đường kính HC.
a) Xét vị trí tương đối của hai đường tròn (O) và (O’).
b) Đường tròn (O) cắt AB tại E, đường tròn (O’) cắt AC tại F. Chứng minh rằng tứ giác AEHF là hình chữ nhật.
c) Chứng minh rằng EF là tiếp tuyến đường tròn (O) và đồng thời là tiếp tuyến đường tròn (O’).
d) Đường trung tuyến AM của tam giác ABC cắt EF tại N. Cho biết AB = 6 cm, AC = 8 cm. Tính diện tích tam giác ANF.
- Chứng minh OO’ = R + R’ và O; H; H’ thẳng hàng suy ra hai đường tròn tiếp xúc nhau.
- Chứng minh \(\widehat {HEA} = {90^o}\) ; \(\widehat {EAF} = {90^o}\); \(\widehat {AFH} = {90^o}\) suy ra AEHF là hình chữ nhật
- Chứng minh EF \( \bot \) OE suy ra EF là đường trung tuyến đường tròn (O) và EF \( \bot \)O’F suy ra EF là đường trung tuyến đường tròn (O’)
- Cần chứng minh \(\frac{{{S_{\Delta ANF}}}}{{{S_{\Delta EAF}}}} = \frac{{A{F^2}}}{{A{H^2}}}\) suy ra \({S_{\Delta ANF}}\)
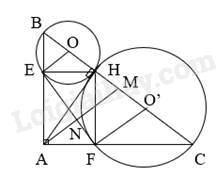
a) Ta có OO’ = OH + O’H = R + R’ suy ra hai đường tròn tiếp xúc nhau.
b) Xét đường tròn (O) có BH là đường kính
\(\widehat {BEH}\) là góc nội tiếp chắn nửa đường tròn suy ra \(\widehat {BEH}\)= 90o hay AB \( \bot \) EH tại E.
Xét đường tròn (O’) có HC là đường kính
\(\widehat {HFC}\) là góc nội tiếp chắn nửa đường tròn suy ra \(\widehat {HFC}\) = 90o hay AC \( \bot \) HF tại F.
Xét tứ giác AEHF có:
\(\widehat {HEA} = {90^o}\) (chứng minh trên);
\(\widehat {EAF} = {90^o}\) (giả thiết);
\(\widehat {AFH} = {90^o}\) (chứng minh trên).
Suy ra tứ giác AEHF là hình chữ nhật.
c) Vì OE = OH = R nên \(\Delta \)OEH cân tại O suy ra \(\widehat {OEH} = \widehat {OHE}\).
Ta có \(\widehat {BHE} = {90^o} - \widehat B\); \(\widehat {BAH} = {90^o} - \widehat B\) suy ra \(\widehat {BHE} = \)\(\widehat {BAH}\).
Mà \(\widehat {OEH} = \widehat {BHE}\) (chứng minh trên); \(\widehat {BAH} = \widehat {AEF}\) (tính chất hình chữ nhật).
Suy ra \(\widehat {OEH} = \widehat {AEF}\) hay \(\widehat {OEH} + \widehat {HEF} = \widehat {AEF} + \widehat {HEF}\) suy ra \(\widehat {OEF} = \widehat {AEH} = {90^o}\).
Nên EF \( \bot \) OE tại E; E \( \in \) (O)
Suy ra EF là đường trung tuyến đường tròn (O) (1).
Vì O’F = O’H = R’ nên tam giác O’HF cân tại O’ suy ra \(\widehat {O'HF} = \widehat {O'FH}\)
Mà \(\widehat {AHF} = \widehat {EFH}\) (tính chất hình chữ nhật)
Nên \(\widehat {O'HF} + \widehat {AFH} = \widehat {O'HF} + \widehat {EFH}\) hay \(\widehat {O'FE} + \widehat {AHC} = {90^o}\).
Nên EF \( \bot \) O’F tại F; F \( \in \) (O’)
Suy ra EF là đường trung tuyến đường tròn (O’) (2).
Từ (1) và (2) ta có điều phải chứng minh.
d) Tam giác ABC vuông tại A có AM là đường trung tuyến, suy ra \({{AM}} = {{BM}} = {{CM}} = \frac{1}{2}{{BC}}\).
Do đó \(\Delta {{AMC}}\) cân tại M , suy ra \(\widehat {{{MAC}}} = \widehat {{{MCA}}}\). (1)
Tam giác \({{O}}'{{FC}}\) cân tại \({{O}}'\) (vì \({{O}}'{{F}} = {{O}}'{{C}}\)) suy ra \(\widehat {{{O}}'{{FC}}} = \widehat {{{O}}'{{CF}}}\).
Suy ra \(\widehat {{{MAC}}} = \widehat {{{O}}'{{FC}}}\).
Mà \(\widehat {{{MAC}}},\widehat {O'FC}\) là hai góc đồng vị nên \({{AM}}//{{O}}'{{F}}\).
Mặt khác \({{O}}'{{F}} \bot {{EF}}\), suy ra \({{AM}} \bot {{EF}}\) tại N .
Xét tam giác ABC vuông tại A có
\({{BC}} = \sqrt {{{A}}{{{B}}^2} + {{A}}{{{C}}^2}} = \sqrt {{6^2} + {8^2}} = 10(\;{{cm}})\)
Diện tích tam giác ABC là
\({{{S}}_{\Delta {{ABC}}}} = \frac{1}{2}{{AH}} \cdot {{BC}} = \frac{1}{2}{{AB}} \cdot {{AC}}\), suy ra \({{AH}} = \frac{{{{AB}} \cdot {{AC}}}}{{{{BC}}}} = \frac{{6 \cdot 8}}{{10}} = 4,8(\;{{cm}})\)
Suy ra \({{EF}} = {{AH}} = 4,8\;{{cm}}\) (vì AEHF là hình chữ nhật).
Xét tam giác AHF và tam giác ACH có:
\(\widehat {AFH} = \widehat {AHC}\left( { = 90^\circ } \right)\)
\(\widehat A\) chung
Suy ra $\Delta \mathrm{AHF} \backsim \Delta \mathrm{ACH}(\mathrm{g} . \mathrm{g})$ nên \(\frac{{{{AH}}}}{{{{AC}}}} = \frac{{{{AF}}}}{{{{AH}}}}\).
Suy ra \({{AF}} = \frac{{{{A}}{{{H}}^2}}}{{{{AC}}}} = \frac{{4,{8^2}}}{8} = 2,88(\;{{cm}})\).
Xét tam giác ANF và tam giác CAB có:
\(\widehat {ANF} = \widehat {CAB}\left( { = 90^\circ } \right)\)
\(\widehat {NAF} = \widehat {ACB}\) (theo (1)
Suy ra $\Delta \text{ANF}\backsim \Delta CAB(\text{g}.\text{g})$
Suy ra \(\frac{{{S_{\Delta {{ANF}}}}}}{{{S_{\Delta CAB}}}} = {\left( {\frac{{AF}}{{BC}}} \right)^2}\)
Diện tích tam giác AFN là:
\({{{S}}_{\Delta AFN}} = {\left( {\frac{{AF}}{{BC}}} \right)^2}.{S_{\Delta CAB}} = {\left( {\frac{{2.88}}{{10}}} \right)^2}.\frac{1}{2}.AB.AC = {\left( {\frac{{2.88}}{{10}}} \right)^2}.\frac{1}{2}.6.8 \approx 2\left( {\;{{c}}{{{m}}^2}} \right)\).

Các bài tập cùng chuyên đề
Bài 1 :
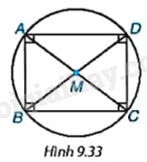
Cho hình chữ nhật ABCD và giao điểm M của hai đường chéo AC và BD (H.9.33).
a) Hãy giải thích vì sao điểm M cách đều bốn đỉnh của hình chữ nhật ABCD.
c) Chứng tỏ rằng hình chữ nhật ABCD nội tiếp một đường tròn có bán kính bằng nửa đường chéo hình chữ nhật.
Bài 2 :
Cho hình thoi ABCD có các cạnh bằng 3cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, AD. Chứng tỏ rằng tứ giác MNPQ là hình chữ nhật và tìm bán kính đường tròn ngoại tiếp của tứ giác đó.
Bài 3 :
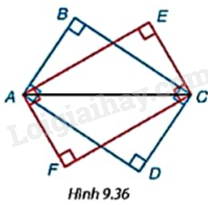
Nếu các hình chữ nhật có chung một đường chéo (ví dụ như hai hình chữ nhật ABCD và AECF trong Hình 9.36) thì các đỉnh của chúng có nằm trên một đường tròn không?
Bài 4 :
Cho hình bình hành ABCD nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình chữ nhật.
Bài 5 :
Tính diện tích của một hình chữ nhật, biết rằng hình chữ nhật đó có chiều dài gấp hai lần chiều rộng và bán kính đường tròn ngoại tiếp bằng 2,5cm.
Bài 6 :
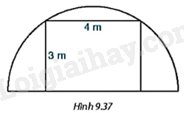
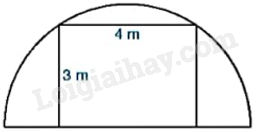
Người ta muốn dựng một khung cổng hình chữ nhật rộng 4m và cao 3m, bên ngoài khung cổng được bao bởi một khung thép dạng nửa đường tròn như Hình 9.37. Tính chiều dài của đoạn thép làm khung nửa đường tròn đó.
Bài 7 :
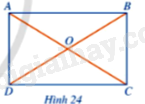
Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?
Bài 8 :
Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 8cm và 6cm. Hình chữ nhật được tô màu xanh còn phần khác của logo được tô màu đỏ. Tính diện tích phần được tô màu đỏ.
Bài 9 :
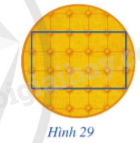
Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng, chiều dài lần lượt là 3 dm, 5 dm. Tính độ dài đường kính mặt trên của tấm đệm, từ đó tính diện tích mặt trên của tấm đệm.
Bài 10 :
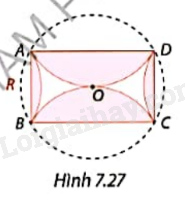
Từ một mảnh giấy có dạng hình tròn bán kính R, bạn Vy gấp lại thành một hình chữ nhật ABCD với chiều rộng AB = R như trong Hình 7.27. Tính tỉ số diện tích của hình chữ nhật gấp được với diện tích mảnh giấy ban đầu. làm tròn kết quả đến hàng phần trăm.
Bài 11 :
Hình chữ nhật có chiều dài gấp đôi chiều rộng nội tiếp trong đường tròn (O;R). Diện tích hình tròn (O;R) là 5\(\pi \)cm2 . Chiều rộng của hình chữ nhật là:
A. 2 cm
B. 3 cm
C. 4 cm
D. 5 cm
Bài 12 :
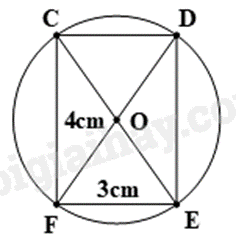
Tính bán kính đường tròn ngoại tiếp hình chữ nhật \(CDEF\) (hình sau).
-
A.
5cm
-
B.
2,5cm
-
C.
4cm
-
D.
4,5cm
Bài 13 :
Cho hình thoi ABCD có AC=8cm, BD=4cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác MNPQ nội tiếp một đường tròn và tìm bán kính của đường tròn đó.
Bài 14 :
Cho hình chữ nhật ABCD nội tiếp (O) với AB=4cm, BC=3cm. Đường tròn (O) có bán kính là
A. R=2,5 cm.
B. R=5 cm.
C. R=1,5 cm.
D. R=2 cm.
Bài 15 :
Cho hình chữ nhật ABCD có \(AB = 3cm,BC = 4cm\) và nội tiếp đường tròn (O; R). Khẳng định nào sau đây là sai?
A. O là trung điểm của AC.
B. O là trung điểm của BD.
C. \(R = 5cm\).
D. \(R = 2,5cm\).
Bài 16 :
Cho hình bình hành ABCD nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình chữ nhật.
Bài 17 :
Tính diện tích của một hình chữ nhật, biết rằng hình chữ nhật đó có chiều dài gấp hai lần chiều rộng và bán kính đường tròn ngoại tiếp bằng 2,5cm.
Bài 18 :
Người ta muốn dựng một khung cổng hình chữ nhật rộng 4m và cao 3m, bên ngoài khung cổng được bao bởi một khung thép dạng nửa đường tròn như hình bên. Tính chiều dài của đoạn thép làm khung nửa đường tròn đó.


















Danh sách bình luận