Cho đường tròn (O), bán kính 5 cm và bốn điểm A, B, C, D thỏa mãn OA = 3 cm, OB = 4 cm, OC = 7 cm, OD = 5 cm. Hãy cho biết mỗi điểm A, B, C, D nằm trong, nằm trên hay nằm ngoài đường tròn (O).
Đọc kĩ dữ liệu để vẽ hình rồi xác định vị trí các điểm.
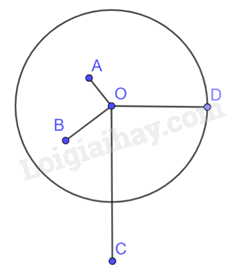
Điểm A, B nằm trong đường tròn (O).
Điểm D nằm trên đường tròn (O).
Điểm C nằm ngoài đường tròn (O).

Các bài tập cùng chuyên đề
Bài 1 :
Cho đường tròn $\left( {O;R} \right)$ và điểm $M$ bất kỳ, biết rằng $OM = R$. Chọn khẳng định đúng?
-
A.
Điểm $M$ nằm ngoài đường tròn
-
B.
Điểm $M$ nằm trên đường tròn
-
C.
Điểm $M$ nằm trong đường tròn
-
D.
Điểm $M$ không thuộc đường tròn.
Bài 2 :
Trên mặt phẳng tọa độ $Oxy$, xác định vị trí tương đối của điểm $A\left( { - 1; - 1} \right)$ và đường tròn tâm là gốc tọa độ $O$, bán kính $R = 2\,$.
-
A.
Điểm $A$ nằm ngoài đường tròn
-
B.
Điểm $A$ nằm trên đường tròn
-
C.
Điểm $A$ nằm trong đường tròn
-
D.
Không kết luận được.
Bài 3 :
Cho đường tròn \(\left( {O;R} \right)\) và điểm \(M\) bất kỳ, biết rằng \(OM > R\). Chọn khẳng định đúng?
-
A.
Điểm \(M\) nằm ngoài đường tròn
-
B.
Điểm \(M\) nằm trên đường tròn
-
C.
Điểm \(M\) nằm trong đường tròn
-
D.
Điểm \(M\) không thuộc đường tròn.
Bài 4 :
Trên mặt phẳng tọa độ \(Oxy\), xác định vị trí tương đối của điểm \(A\left( { - 3; - 4} \right)\) và đường tròn tâm là gốc tọa độ \(O\), bán kính \(R = 3\).
-
A.
Điểm \(A\) nằm ngoài đường tròn
-
B.
Điểm \(A\) nằm trên đường tròn
-
C.
Điểm \(A\) nằm trong đường tròn
-
D.
Không kết luận được.
Bài 5 :
Trong mặt phẳng tọa độ Oxy, cho các điểm A(3;0), B(- 2;0), C(0;4). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn (O; 3)?
Bài 6 :
Trong mặt phẳng tọa độ Oxy, cho các điểm M (0 ; 2), N (0; -3) và P(2; -1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn \(\left( {O;\sqrt 5 } \right)\)? Vì sao?
Bài 7 :
Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Bài 8 :
Cho đường tròn (O; 4 cm) và hai điểm A, B. Biết rằng OA = \(\sqrt {15} \)cm và OB = 4 cm. Khi đó:
A. Điểm A nằm trong (O), điểm B nằm ngoài (O).
B. Điểm A nằm ngoài (O), điểm B nằm trên (O).
C. Điểm A nằm trên (O), điểm B nằm trong (O).
D. Điểm A nằm trong (O), điểm B nằm trên (O).
Bài 9 :
Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Bài 10 :
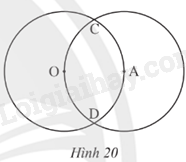
Cho hai đường tròn (O; 2 cm) và (A; 2 cm) cắt nhau tại C, D, điểm A nằm trên đường tròn tâm O (Hình 20).
a) Vẽ đường tròn (C; 2 cm)
b) Đường tròn (C; 2 cm) có đi qua hai điểm O và A không? Vì sao?
Bài 11 :
Trong các điểm sau, điểm nào nằm trên đường tròn (O; 2cm).
-
A.
Điểm \(A\left( { - 1; - 1} \right)\).
-
B.
Điểm \(B\left( { - 1; - 2} \right)\).
-
C.
Điểm \(C\left( {\sqrt 2 ;\sqrt 2 } \right)\).
-
D.
Điểm \(D\left( {1; - 2} \right)\).
Bài 12 :
Cho đường tròn \(\left( {O;5cm} \right)\) hai điểm A, B. Biết rằng \(OA = \sqrt {26} \) và \(OB = \frac{{17}}{4}\). Khi đó:
-
A.
Điểm A nằm trong (O), điểm B nằm ngoài (O).
-
B.
Điểm A nằm ngoài (O), điểm B nằm trong (O).
-
C.
Điểm A nằm trên (O), điểm B nằm trong (O).
-
D.
Điểm A nằm trong (O), điểm B nằm trong (O).
Bài 13 :
Cho tam giác đều ABC cạnh bằng a, các đường cao là BM và CN. Gọi D là trung điểm của cạnh BC. Gọi G là giao điểm của BM và CN. Xác định vị trí tương đối của điểm G và điểm A với đường tròn đi qua bốn điểm B, N, M, C.
-
A.
Điểm G nằm ngoài đường tròn, điểm A nằm trong đường tròn.
-
B.
Điểm G nằm trong đường tròn, điểm A nằm ngoài đường tròn.
-
C.
Điểm G và điểm A nằm trong đường tròn.
-
D.
Điểm G và điểm A nằm ngoài đường tròn.
Bài 14 :
Cho đường tròn (O) có bán kính bằng 2,5cm và hai tia Ox, Oy vuông góc với nhau tại O. Trên tia Ox lấy điểm A sao cho \(OA = 3cm\); trên tia Oy lấy điểm B sao cho \(OB = 4cm\). Gọi M là trung điểm của đoạn AB. Chứng minh rằng điểm M nằm trên đường tròn (O).
Bài 15 :
Trên mặt phẳng tọa độ Oxy, cho hai điểm A(0; -3) và B(2; 0). Gọi C và D là các điểm lần lượt đối xứng với A và B qua O.
a) Xác định tọa độ của hai điểm C và D.
b) Xác định vị trí của các điểm A, B, C và D đối với đường tròn (O; 3).
Bài 16 :
Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 1). Gọi B, C và D là các điểm đối xứng với A lần lượt qua trục hoành, qua gốc O và qua trục tung.
a) Xác định tọa độ của ba điểm B, C và D.
b) Có hay không một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm và bán kính của đường tròn đó, nếu có.
Bài 17 :
Cho đường tròn (O), đường kính AB và điểm M thuộc (O) (M không trùng với điểm nào trong hai điểm A và B). Trên (O) lấy điểm N nằm khác phía của M đối với đường thẳng AB sao cho \(AM = BN\). Chứng minh rằng O là trung điểm của đoạn MN.
Bài 18 :
Trong mặt phẳng tọa độ Oxy, cho đường tròn (O; \(\sqrt 5 \)), hai điểm \(A\left( { - \sqrt 3 ;1} \right)\) và B(-1; 2). Khi đó xảy ra:
A. Điểm A nằm trong (O), điểm B nằm ngoài (O).
B. Điểm A nằm trong (O), điểm B nằm trên (O).
C. Điểm A nằm trên (O), điểm B nằm trong (O).
D. Điểm A nằm ngoài (O), điểm B nằm trên (O).
Bài 19 :
Cho đường thẳng xy cắt đường tròn (O) tại hai điểm A và B (H.5.10). Khi đó, các điểm thuộc đường thẳng xy và nằm trong đường tròn (O) là:
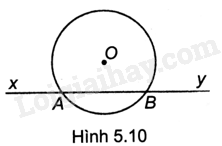
A. Các điểm thuộc tia AB.
B. Các điểm thuộc tia By.
C. Các điểm thuộc đoạn AB.
D. Các điểm nằm giữa A và B.
Bài 20 :
Cho tam giác ABC có AB = AC = 13 cm, Bc = 10 cm và có BH, CK là hai đường cao. Chứng minh:
a) Bốn điểm B, C, H, K cùng nằm trên đường tròn (O;R).
b) Điểm A nằm ngoài đường tròn (O; R).
Bài 21 :
Trên mặt phẳng tọa độ Oxy, cho các điểm A(-1; -1), B(-1; -2), C\(\left( {\sqrt 2 ;\sqrt 2 } \right)\) và đường tròn tâm O bán kính 2cm. Khẳng định nào sau đây là sai?
A. Điểm A nằm trong đường tròn (O; 2).
B. Điểm B nằm trên đường tròn (O; 2).
C. Điểm C nằm trên đường tròn (O; 2).
D. Điểm B nằm ngoài đường tròn (O; 2).
Bài 22 :
Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H. Khẳng định nào sau đây là đúng?
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn.
B. Bốn điểm A, E, H, D cùng nằm trên một đường tròn.
C. \(DE < BC\).
D. Cả ba đáp án trên đều đúng.
Bài 23 :
Trong mặt phẳng tọa độ Oxy, cho các điểm M(0; 2), N (0; -3) và P(2; -1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn (O; \(\sqrt 5 \))? Vì sao?
Bài 24 :
Cho tam giác ABC vuông tại A có \(AB = 3cm,AC = 4cm\). Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Bài 25 :
Cho đường tròn (O; 4cm) và hai điểm A, B. Biết \(OA = \sqrt {15} cm\) và \(OB = 4cm\). Khi đó:
A. Điểm A nằm trong (O), điểm B nằm ngoài (O).
B. Điểm A nằm ngoài (O), điểm B nằm trên (O).
C. Điểm A nằm trên (O), điểm B nằm trong (O).
D. Điểm A nằm trong (O), điểm B nằm trên (O).
Bài 26 :
Cho đường tròn \(\left( {O;3\;{\rm{cm}}} \right)\) và hai điểm A,B thỏa mãn \(OA = 3\;{\rm{cm}},OB = 4\;{\rm{cm}}\). Khẳng định nào sau đây đúng?-
A.
Điểm \(A\) nằm trong \(\left( O \right)\), điểm \(B\) nằm ngoài \(\left( O \right)\)
-
B.
Điểm \(A\) nằm ngoài \(\left( O \right)\), điểm \(B\) nằm trên \(\left( O \right)\)
-
C.
Điểm \(A\) nằm trên \(\left( O \right)\), điểm \(B\) nằm ngoài \(\left( O \right)\)
-
D.
Điểm \(A\) nằm trên \(\left( O \right)\), điểm \(B\) nằm trong \(\left( O \right)\)


















Danh sách bình luận