Cho một hình trụ có đường kính của đáy bằng với chiều cao và có thể tích bằng \(2\pi \;c{m^3}\).
a) Tính chiều cao của hình trụ.
b) Diện tích toàn phần của hình trụ bằng tổng diện tích xung quanh và diện tích hai đáy trụ. Tính diện tích toàn phần của hình trụ trên.
a) + Gọi đường kính đáy của hình trụ là R. Tính bán kính đáy và chiều cao của hình trụ theo R.
+ Tính thể tích hình trụ theo R, cho biểu thức đó bằng \(2\pi \), từ đó giải phương trình tìm R.
b) + Diện tích xung quanh của hình trụ có bán kính đáy R và chiều cao h là: \({S_{xq}} = 2\pi Rh\).
+ Diện tích hai đáy hình trụ bán kính R là: \({S_1} = 2.\pi {R^2}\).
+ Diện tích toàn phần hình trụ: \(S = {S_{xq}} + {S_1}\).
a) Gọi đường kính đáy của hình trụ là R (\(R > 0\), cm).
Khi đó, bán kính đáy của hình trụ là \(\frac{R}{2}\left( {cm} \right)\) và chiều cao là R (cm).
Thể tích hình trụ là:
\(V = \pi .{\left( {\frac{R}{2}} \right)^2}.R = \frac{{{R^3}\pi }}{4}\).
Vì thể tích hình trụ bằng \(2\pi \;c{m^3}\) nên ta có: \(\frac{{{R^3}\pi }}{4} = 2\pi \), suy ra \({R^3} = 8\) nên \(R = 2cm\) (do \(R > 0\))
Vậy chiều cao hình trụ là: \(h = 2cm\).
b) Diện tích xung quanh của hình trụ bán kính 1cm và chiều cao 2cm là:
\({S_{xq}} = 2\pi .1.2 = 4\pi \left( {c{m^2}} \right)\).
Diện tích hai đáy của hình trụ bán kính 1cm là:
\({S_1} = 2.\pi {.1^2} = 2\pi \left( {c{m^2}} \right)\).
Diện tích toàn phần của hình trụ là:
\(S = {S_{xq}} + {S_1} = 4\pi + 2\pi = 6\pi \left( {c{m^2}} \right)\).

Các bài tập cùng chuyên đề
Bài 1 :
Một thùng nước có dạng hình trụ với chiều cao bằng 1,6m và bán kính đáy bằng 0,5m.
a) Tính diện tích xung quanh của thùng nước.
b) Hỏi thùng nước chứa được bao nhiêu lít nước?
(Coi chiều dày của thùng không đáng kể và làm tròn kết quả ở câu b đến hàng đơn vị của lít).
Bài 2 :
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:
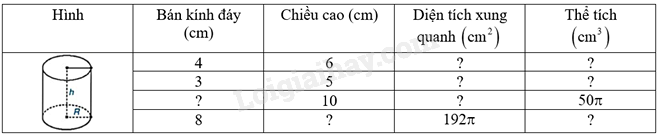
Bài 3 :
Cho hình chữ nhật ABCD có \(AB = 3cm,BC = 4cm\). Quay hình chữ nhật quanh cạnh AB một vòng, ta được một hình trụ. Tính diện tích xung quanh và thể tích của hình trụ tạo thành.
Bài 4 :
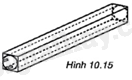
Một bóng đèn huỳnh quang có dạng hình trụ được đặt khít vào một hộp giấy cứng dạng hình hộp chữ nhật (H.10.15). Hộp giấy có chiều dài bằng 0,6m, đáy là hình vuông cạnh 4cm. Tính diện tích xung quanh và thể tích của bóng đèn (giả sử bề dày của hộp giấy không đáng kể).
Bài 5 :
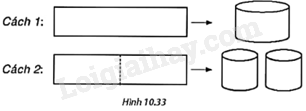
Từ một tấm tôn hình chữ nhật có kích thước \(50cm \times 240cm\), người ta làm mặt xung quanh của các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (H.10.33):
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng nước hình trụ.
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau hình chữ nhật, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu \({V_1}\) là thể tích của thùng gò được theo Cách 1 và \({V_2}\) là tổng thể tích của hai thùng gò được theo Cách 2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) (giả sử các mối hàn là không đáng kể).
Bài 6 :
Cho hình trụ có bán kính đáy bằng 20cm, chiều cao bằng 30cm.
a) Tính diện tích xung quanh của hình trụ.
b) Tính thể tích của hình trụ.
Bài 7 :
Đèn trời có dạng hình trụ không có một đáy với đường kính đáy bằng 0,8m và thân đèn cao 1m. Tính diện tích giấy dán bên ngoài đèn trời.

Bài 8 :
Tìm chiều cao, bán kính đáy và diện tích xung quanh, thể tích của mỗi hình trụ sau:
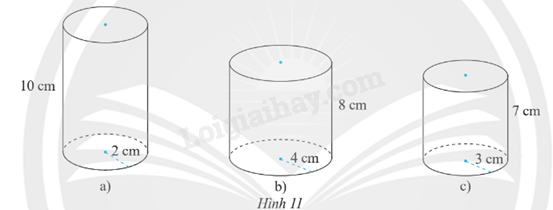
Bài 9 :
Trong một hình trụ
A. độ dài của đường sinh là chiều cao của hình trụ.
B. đoạn nối hai điểm bất kì trên hai đáy là đường sinh.
C. chiều cao là độ dài đoạn nối hai điểm bất kì trên hai đáy.
D. hai đáy có độ dài bán kính bằng nhau
Bài 10 :
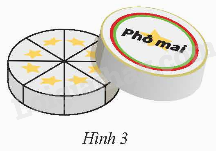
Hộp phô mai hình trụ có đường kính đáy 12,2 cm, chiều cao 2,4 cm.
a) Biết rằng 8 miếng phô mai được xếp nằm sát nhau vừa khít trong hộp (Hình 3). Hỏi thể tích một miếng phô mai là bao nhiêu?
b) Người ta gói từng miếng phô mai bằng một loại giấy đặc biệt. Giả sử phần giấy gói vừa khít miếng phô mai. Hãy tính diện tích phần giấy gói mỗi miếng phô mai.
Bài 11 :
Pin là nguồn năng lượng phổ biến được sử dụng trong nhiều dụng cụ và thiết bị trong gia đình. Pin AAA (hay pin 3A) là một loại pin khô, thường được dùng trong những thiết bị điện tử cầm tay, chẳng hạn, điều khiển từ xa ti vi, máy nghe nhạc MP3, ... Mỗi chiếc pin 3A có dạng hình trụ (Hình 15), với kích cỡ tiêu chuẩn: chiều cao khoảng 44,5 mm và đường kính đáy khoảng 10,5 mm. Tính diện tích xung quanh, diện tích toàn phần (theo đơn vị centimét vuông) và thể tích (theo đơn vị centimét khối) của một chiếc pin 3A đó (làm tròn kết quả đến hàng phần mười).
Bài 12 :
Tính chiều cao và thể tích của một hình trụ có bán kính đáy bằng 5 cm và diện tích xung quanh bằng \(30\pi \)cm2.
Bài 13 :
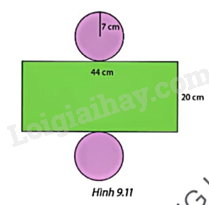
Tính diện tích xung quanh và thể tích của hình trụ có hình khai triển như Hình 9.11. Lấy \(\pi \approx \frac{{22}}{7}\).
Bài 14 :
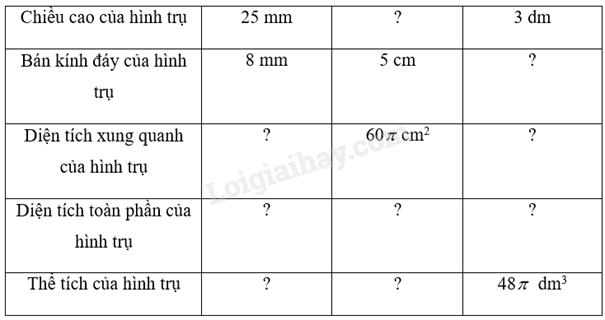
Tìm các số và đơn vị thích hợp trong các ô ? để hoàn thành Bảng 9.1.
Bài 15 :
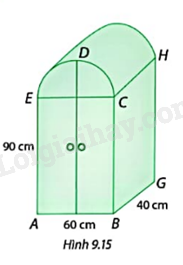
Hình 9.15 là một tủ chứa đồ. Biết cung CDE là nửa đường tròn.
a) Tính thể tích của tủ đồ.
b) Người ta muốn sơn tất cả các mặt ngoài của tủ (kể cả đáy). Hỏi diện tích cần sơn là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
Bài 16 :
Chọn câu đúng. Cho hình trụ có bán kính đáy \(R\) và chiều cao \(h\). Nếu ta giảm chiều cao đi chín lần và tăng bán kính đáy lên ba lần thì:
-
A.
Thể tích hình trụ không đổi.
-
B.
Diện tích toàn phần không đổi.
-
C.
Diện tích xung quanh không đổi.
-
D.
Chu vi đáy không đổi.
Bài 17 :
Một bể nước hình trụ có bán kính đáy \(R = 1,2\,m\) (tính từ tâm bể đến mép ngoài), bề dày của thành bể là \(b = 0,05m\), chiều cao của lòng bể \(h = 1,26m\) (Lấy \(\pi = 3,14\) và kết quả làm tròn tới độ chính xác 0,005)
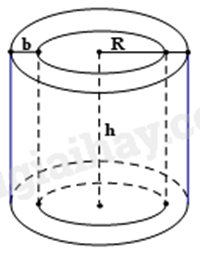
a) Bán kính bên trong lòng bể nước là \(1,15\;m\).
b) Dung tích của bể nước là \(5,25\;{m^3}\).
c) Ban đầu bể không có nước. Sau đó người ta bơm nước vào bể với tốc độ \(1\) lít/giây. Sau 20 phút bơm vào bể thì nước bị tràn nước ra ngoài bể.
d) Biết độ dày của đáy bể là \(d = 0,08m\). Để hoàn thành một cái bể đó thì cần khoảng \(0,827\;{m^3}\) bê tông.
Bài 18 :
Bác Tú cần làm 10 khối bê tông hình trụ bao quanh ở các gốc cây trong vườn. Biết bề dày của khối bê tông là 9cm, chiều cao 10cm và đường kính đáy của hình trụ lớn là 90cm (như hình vẽ). (lấy \(\pi = 3,14\) )
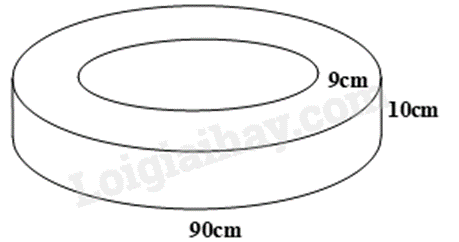
a) Bán kính đáy hình trụ bên trong khối bê tông là 36cm.
b) Thể tích hình trụ bên trong khối bê tông là: \(40694,4{\rm{ }}\left( {c{m^3}} \right)\).
c) Thể tích hình trụ bên ngoài khối bê tông là: \(63580{\rm{ }}\left( {c{m^3}} \right)\).
d) Tính thể tích vữa cần dùng để thực hiện 10 khối bê tông trên là 228906 (cm3).
Bài 19 :
Một cái mũ bằng vải của nhà ảo thuật với kích thước như hình vẽ.
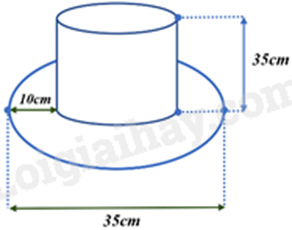
a) Bán kính đáy là 7,0cm.
b) Diện tích vải để làm ống mũ là \(581,25\pi \left( {c{m^2}} \right)\).
c) Diện tích vải để làm vành mũ là: \(240\pi \left( {c{m^2}} \right)\).
d) Tổng diện tích vải cần để làm cái mũ đó. Biết rằng tỉ lệ vải khâu (may) hao (tốn) khi may mũ là 12%. Cho biết \(\pi = 3,14\) (làm tròn đến hàng đơn vị) là \(2925\left( {c{m^2}} \right)\).
Bài 20 :
Bạn Linh muốn đặt thợ làm bánh sinh nhật có 2 tầng. Tầng bánh phía trên cao \(15\;cm\), bán kính tầng trên là \(15\;cm\). Tầng phía dưới cao \(20\;cm\) và đường kính tầng dưới là \(40\;cm\).
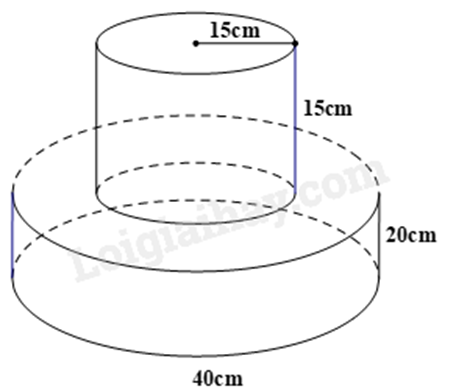
a) Tầng phía dưới của bánh sinh nhật cao hơn tầng phía trên là \(5\;cm\).
b) Thể tích phần bánh tầng dưới lớn hơn tầng trên là \(4625\pi \;c{m^3}\).
c) Diện tích mặt đáy tầng dưới gấp 1,5 lần diện tích mặt đáy tầng trên.
d) Người thợ muốn phủ một lớp kem trên mặt ngoài của bánh để trang trí (mặt đáy bánh không trang trí). Diện tích phần trang trí khoảng \(5181\;c{m^2}\). (lấy \(\pi \approx 3,14\) )
Bài 21 :
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:

Bài 22 :
Bác Thu có một khối gỗ dạng hình trụ, chiều cao bằng 30cm, đường kính đáy bằng 20cm. Bác dự định sơn kín mặt ngoài của khối gỗ. Tính diện tích phần cần sơn (làm tròn kết quả đến hàng phần mười của \(c{m^2}\)).
Bài 23 :
Một khối gỗ có dạng hình trụ, chiều cao bằng 50cm, đường kính đáy bằng 30cm.
a) Tính thể tích của khối gỗ.
b) Nếu sơn phủ kín mặt bên ngoài khối gỗ thì diện tích cần sơn là bao nhiêu (làm tròn kết quả đến hàng đơn vị của \(c{m^2}\))?
Bài 24 :
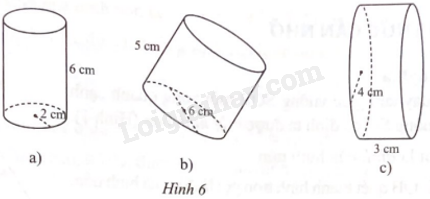
Tính diện tích xung quanh và thể tích của mỗi hình trụ sau:
Bài 25 :
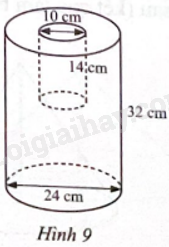
Từ một hình trụ có đường kính đáy 24 cm và chiều cao 32 cm, người ta khoét bỏ một hình trụ có đường kính đáy 10 cm và chiều cao 14 cm (Hình 9).
a) Tính thể tích của phần còn lại của hình trụ.
b) Người ta sơn toàn bộ các mặt của phần còn lại của hình trụ. Tính diện tích được phủ sơn (kết quả làm tròn đến hàng đơn vị của xăngtimet vuông).
Bài 26 :
Trong các phát biểu sau, phát biểu nào đúng?
A. Diện tích xung quanh của hình trụ bằng tích của diện tích đáy với chiều cao.
B. Diện tích toàn phần của hình trụ bằng tổng của diện tích xung quanh và diện tích một mặt đáy.
C. Diện tích xung quanh của hình trụ bằng tích của chu vi đáy với chiều cao.
D. Thể tích của hình trụ bằng một phần ba tích của diện tích đáy với chiều cao.
Bài 27 :
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:

Bài 28 :
Cho hình chữ nhật ABCD có \(AB = 3cm,BC = 4cm\). Quay hình chữ nhật quanh cạnh AB một vòng, ta được một hình trụ. Tính diện tích xung quanh và thể tích của hình trụ tạo thành.
Bài 29 :
Một bóng đèn huỳnh quang có dạng hình trụ được đặt khít vào một hộp giấy cứng dạng hình hộp chữ nhật. Hộp giấy có chiều dài bằng 0,6m, đáy là hình vuông cạnh 4cm. Tính diện tích xung quanh và thể tích của bóng đèn (giả sử bề dày của hộp giấy không đáng kể).
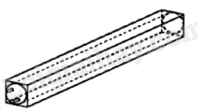
Bài 30 :
Một khối gỗ có dạng hình trụ có bán kính đáy là 30cm và chiều cao là 120cm.
a) Tính thể tích của khối gỗ đó (làm tròn kết quả tới hàng phần trăm của \(c{m^3}\)).
b) Nếu sơn kín các mặt của khối gỗ thì diện tích cần sơn bằng bao nhiêu? (Làm tròn kết quả tới hàng đơn vị của \(c{m^2}\)).


















Danh sách bình luận