Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như Hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?
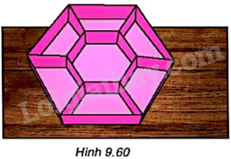
- Gọi O là tâm đa giác lớn và đa giác nhỏ.
- Dựa vào kiến thức về lục giác đều, ta có hình lục giác được chia thành 6 tam giác đều chung đỉnh O, 2 đỉnh còn lại là các đỉnh 2 đỉnh kề nhau của lục giác.
- Lấy hai điểm A, B là hai đỉnh kề nhau của lục giác nhỏ như hình vẽ. Đặt AB = x (cm). Khi đó ta có \(\Delta AOB\) đều.
- Kẻ \(OH \bot AB\), tính đường cao OH của tam giác AOB. Từ đó ta tính được \({S_{\Delta AOB}}\).
Từ đó ta tính được diện tích hình lục giác đều nhỏ: Slục giác đều nhỏ \( = 6.{S_{\Delta AOB}}\).
Vì diện tích lục giác đều nhỏ bằng hai lần diện tích mỗi hình thang nên diện tích mỗi hình thang là:
Shình thang = Slục giác đều nhỏ : 2, suy ra tổng diện tích 6 hình thang.
Ta tính được Slục giác đều lớn = Slục giác đều nhỏ + S6 hình thang.
Mà ta còn tính được diện tích hình lục giác đều lớn qua cạnh của nó giống như Slục giác đều nhỏ.
Từ đó giải phương trình để tìm x.
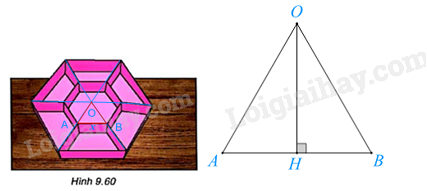
Nối các cặp đỉnh đối diện của lục giác với nhau, ta được điểm O là tâm của hình lục giác lớn và lục giác nhỏ.
Ta chia hình lục giác thành 6 tam giác đều chung đỉnh O, 2 đỉnh còn lại là các đỉnh 2 đỉnh kề nhau của lục giác.
Lấy hai điểm A, B là hai đỉnh kề nhau của lục giác nhỏ như hình vẽ. Đặt AB = x (cm) \(\left( {0 < x < 10} \right)\).
Khi đó \(\Delta AOB\) đều có \(OA = OB = AB = x\) và \(\widehat B = 60^\circ \).
Kẻ \(OH \bot AB\). Dựa vào hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
\(OH = OB.\sin \widehat {OBA} = x.\sin 60^\circ = \frac{{\sqrt 3 }}{2}x\left( {cm} \right)\)
Suy ra \({S_{\Delta AOB}} = \frac{{OH.AB}}{2} = \frac{{\frac{{\sqrt 3 }}{2}x.x}}{2} = \frac{{{x^2}\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Ta có diện tích hình lục giác đều nhỏ là:
Slục giác đều nhỏ \( = 6.{S_{\Delta AOB}} = 6.\frac{{{x^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\).
Theo đề bài, diện tích lục giác đều nhỏ bằng hai lần diện tích mỗi hình thang nên diện tích mỗi hình thang là:
Shình thang = Slục giác đều nhỏ : 2 = \(\frac{{3\sqrt 3 {x^2}}}{2}:2 = \frac{{3\sqrt 3 {x^2}}}{4}\left( {c{m^2}} \right)\),
suy ra tổng diện tích 6 hình thang là: \(6.\frac{{3\sqrt 3 {x^2}}}{4} = \frac{{9\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\)
Do đó, diện tích lục giác đều lớn là:
Slục giác đều lớn = Slục giác đều nhỏ + S6 hình thang \( = \frac{{3\sqrt 3 {x^2}}}{2} + \frac{{9\sqrt 3 {x^2}}}{2} = \frac{{12\sqrt 3 {x^2}}}{2} = 6\sqrt 3 {x^2}\left( {c{m^2}} \right)\) (1)
Mà tương tự như Slục giác đều nhỏ, ta cũng có thể tính được diện tích lục giác đều theo độ dài cạnh của nó theo công thức \(S = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\) với x là độ dài cạnh.
Suy ra Slục giác đều lớn \( = \frac{{3\sqrt 3 {{.10}^2}}}{2} = 150\sqrt 3 \left( {c{m^2}} \right)\) (2)
Từ (1) và (2), ta có phương trình: \(6\sqrt 3 {x^2} = 150\sqrt 3 \)
suy ra \({x^2} = 25\), do đó \(x = 5\)(thỏa mãn vi \(0 < x < 10\)).
Vậy cạnh của lục giác đều nhỏ là 5cm.

Các bài tập cùng chuyên đề
Bài 1 :
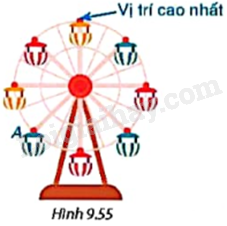
Cho vòng quay mặt trời gồm tám cabin như Hình 9.55. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm bao nhiêu độ?
Bài 2 :
Hãy tìm hiểu trong tự nhiên hay trong nghệ thuật, trang trí, thiết kế, công nghệ,… những vật thể mà cấu trúc của nó có dạng hình đa giác đều.
Bài 3 :
Thiết kế một đồ vật từ những hình có dạng đa giác đều. Chẳng hạn, vẽ trên giấy 20 hình tam giác đều bằng nhau rồi cắt ra và dán lại để tạo thành hình chao đèn (hình 20 mặt đều), như ở hình 22.

Bài 4 :
Tìm hiểu và chỉ ra những vật thể trong thực tiễn mà cấu trúc của nó có dạng hình đa giác đều.
Bài 5 :
Gọi tên các đa giác đều có trong Hình 8.6.

Bài 6 :
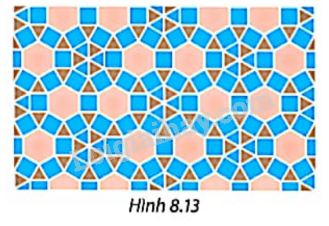
Kể tên các loại đa giác đều trong hoạ tiết ở Hình 8.13.
Bài 7 :
Hãy tìm thêm một số hình phẳng đều khác trong thực tiễn.
Bài 8 :
Kể tên các loại các loại đa giác đều trong mỗi trường hợp ở Hình 8.17.

Bài 9 :
Lâu đài Castel del Monte ở Ý có kiến trúc độc đáo với đáy và giếng trời đều là bát giác đều. Tính chu vi đáy của lâu đài (không tính các tháp canh), biết cạnh đáy dài khoảng 16,5 m.

Bài 10 :
Lâu đài Castel del Monte ở Ý có kiến trúc với đáy và giếng trời là có dạng hình gì?
-
A.
Tam giác đều.
-
B.
Bát giác đều.
-
C.
Lục giác đều.
-
D.
Ngũ giác đều.
Bài 11 :
Mái nhà trong hình vẽ dưới đây được đỡ bởi khung hình đa giác đều. Gọi tên đa giác đó

-
A.
Đa giác đều 12 cạnh.
-
B.
Đa giác đều 8 cạnh.
-
C.
Đa giác đều 10 cạnh.
-
D.
Đa giác đều 4 cạnh.
Bài 12 :
Hình ảnh tổ ong có liên quan đến đa giác đều nào sau đây?
-
A.
Tam giác đều.
-
B.
Tứ giác đều.
-
C.
Ngũ giác đều.
-
D.
Lục giác đều.
Bài 13 :
Ngũ giác đài hay Lầu năm góc là trụ sở Bộ Quốc phòng Hoa Kỳ có dạng hình ngũ giác đều với độ dài cạnh khoảng 280 m như Hình 12. Tính khoảng cách từ tâm đối xứng đến một cạnh của ngũ giác đều này (kết quả làm tròn đến hàng phần mười của mét).



















Danh sách bình luận