Cho tam giác ABC đều có trọng tâm G.
a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC.
b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).
a) Sử dụng tính chất: Trong tam giác đều, trọng tâm đồng thời là giao điểm của ba đường phân giác. Suy ra, G là tâm đường tròn nội tiếp tam giác ABC.
b) + Gọi D là giao điểm của AG và CB. Khi đó, GD là bán kính đường tròn đường tròn nội tiếp tam giác ABC, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
+ Theo tính chất của trọng tâm trong tam giác ABC ta có: \(GD = \frac{1}{2}AG = \frac{1}{3}AD\).
+ Theo định lí Pythagore vào tam giác ADC vuông tại D tính được: \(AD = \frac{{BC\sqrt 3 }}{2}\), nên \(GD = \frac{{\sqrt 3 }}{6}BC\).
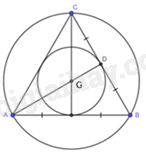
a) Tam giác ABC đều nên G là trọng tâm của tam giác ABC đồng thời là giao điểm của ba đường phân giác. Do đó, G là tâm đường tròn nội tiếp tam giác ABC.
b) Vì G là giao điểm của ba đường trung trực trong tam giác đều ABC (do G là trọng tâm tam giác ABC) nên G là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi D là giao điểm của AG và CB. Suy ra, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
Tam giác ABC đều nên AD là đường trung tuyến đồng thời là đường cao trong tam giác. Do đó, \(GD \bot CB\) tại D. Suy ra, GD là bán kính đường tròn nội tiếp tam giác ABC.
Vì G là trọng tâm tam giác ABC nên \(GD = \frac{1}{2}AG = \frac{1}{3}AD\).
Áp dụng định lí Pythagore vào tam giác ADC vuông tại D có:
\(A{D^2} + C{D^2} = A{C^2} \Rightarrow AD = \sqrt {A{C^2} - C{D^2}} = \sqrt {B{C^2} - \frac{{B{C^2}}}{4}} = \frac{{BC\sqrt 3 }}{2}\)
Do đó, \(GD = \frac{1}{3}.\frac{{BC\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{6}BC\).
Vậy bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác đều ABC (H.9.22).
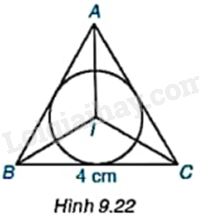
a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC.
b) Biết rằng \(BC = 4cm\), hãy tính bán kính r.
Bài 2 :
Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1cm.
Bài 3 :
Người ta muốn làm một khung gỗ tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30cm (H.9.23). Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?

Bài 4 :
Tính diện tích tam giác đều có bán kính đường tròn nội tiếp bằng 1 cm.
Bài 5 :
Cho tam giác đều ABC có đường cao AH = 9 cm. Bán kính r của đường tròn nội tiếp tam giác có độ dài là
A. 6 cm.
B. 3 cm.
C. 4,5 cm.
D. \(\frac{{3\sqrt 3 }}{2}\) cm.
Bài 6 :
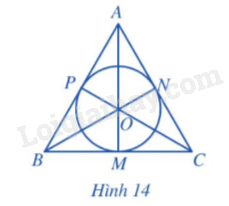
Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 14).
a) AM, BN, CP có là các đường phân giác của tam giác ABC hay không?
b) Điểm O có là tâm đường tròn nội tiếp tam giác ABC hay không?
c) Tính OM theo a.
Bài 7 :
Cho tam giác đều ABC ngoại tiếp đường tròn (O; 6). Tính AB.
Bài 8 :
Cho bán kính đường tròn nội tiếp tam giác đều bằng 4cm. Tính cạnh của tam giác đều đó.
Bài 9 :
Một chiếc đồng hồ trong Hình 7.9 có đường viền là một đường tròn tiếp xúc với ba cạnh của khung đồng hồ hình tam giác đều. Đường kính của đường viền mặt đồng hồ là 10 cm. Khung hình tam giác đều của đồng hồ có độ dài cạnh là bao nhiêu centimet (độ dày đường viền của khung không đáng kể)? Làm tròn kết quả đến hàng phần mười.

Bài 10 :
Bạn Tú muốn đặt một chiếc bánh hình tròn vào chính giữa một chiếc hộp có mặt là hình tam giác đều như Hình 7, 24. Đường kính tối đa của chiếc bánh là bao nhiêu centimet nếu cạnh đáy của hộp là 8 cm? Làm tròn kết quả đến hàng phần mười.

Bài 11 :
Đường tròn nội tiếp của một tam giác đều có đường kính \(20\sqrt 3 \) cm. Độ dài cạnh của tam giác đều bằng
A. 45 cm
B. 60 cm
C. 90 cm
D. 120 cm
Bài 12 :
Cho $\Delta ABC$ đều ngoại tiếp đường tròn $\left( O,10cm \right)$. Tính độ dài cạnh của tam giác đều.
-
A.
$20\sqrt{3}$
-
B.
$30\sqrt{3}$
-
C.
$\frac{3\sqrt{3}}{20}$
-
D.
$\frac{\sqrt{6}}{20}$
Bài 13 :
Người ta muốn làm một khung gỗ hình tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 40cm. Độ dài các cạnh (phía bên trong) của khung gỗ là ...cm (Làm tròn kết quả đến hàng đơn vị).
Bài 14 :
Tính chu vi và diện tích của tam giác đều ngoại tiếp một đường tròn bán kính 3cm.
Bài 15 :
Cho tam giác ABC ngoại tiếp đường tròn (I). Chứng minh rằng:
\(\widehat {BIC} = {90^o} + \frac{{\widehat {BAC}}}{2};\widehat {CIA} = {90^o} + \frac{{\widehat {CBA}}}{2};\widehat {AIB} = {90^o} + \frac{{\widehat {ACB}}}{2}\).
Bài 16 :
Tam giác đều cạnh bằng \(8a\sqrt 3 \) có bán kính đường tròn nội tiếp là
A. 4a
B. 2a
C. \(4a\sqrt 3 \)
D. \(2a\sqrt 3 \)
Bài 17 :
Người ta muốn làm một khung gỗ tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30cm như hình bên. Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?

Bài 18 :
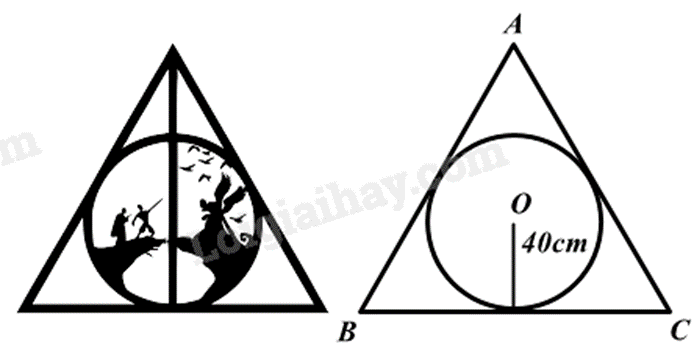
Một bức ảnh hình tròn có bán kính 40 cm, người ta làm một khung gỗ hình tam giác đều bao bên ngoài bức ảnh sao cho bức ảnh hình tròn tiếp xúc với các cạnh của khung gỗ. Tính độ dài cạnh khung gỗ (làm tròn đến số thập phân thứ nhất).
Bài 19 :
Tính bán kính đường tròn nội tiếp của tam giác đều có cạnh bằng 16cm.
-
A.
\(4\sqrt 3 \)cm.
-
B.
\(8\sqrt 3 \)cm.
-
C.
\(\frac{{8\sqrt 3 }}{3}\)cm.
-
D.
\(\frac{{16\sqrt 3 }}{3}\)cm.
Bài 20 :
Cho bán kính của đường tròn nội tiếp tam giác đều là \(\frac{{\sqrt 3 }}{2}cm\). Độ dài cạnh của tam giác đều đó là:
-
A.
\(\frac{3}{2}cm\).
-
B.
\(\frac{{3\sqrt 3 }}{2}cm\).
-
C.
\(3cm\).
-
D.
\(\sqrt 3 cm\).


















Danh sách bình luận