Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau:
E: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 11”;
F: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 hoặc 9”;
G: “Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 6”.
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Ta có bảng miêu tả không gian mẫu là:
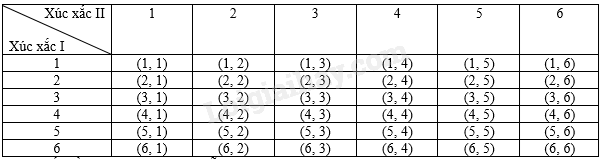
Do đó, số phần tử của không gian mẫu \(\Omega \) là 36.
Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng.
Có 2 kết quả thuận lợi của biến cố E là: (5, 6), (6, 5). Do đó, \(P\left( E \right) = \frac{2}{{36}} = \frac{1}{{18}}\).
Có 9 kết quả thuận lợi của biến cố F là: (2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (5, 3), (5, 4), (6, 2), (6, 3). Do đó, \(P\left( F \right) = \frac{9}{{36}} = \frac{1}{4}\).
Có 10 kết quả thuận lợi của biến cố G là: (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1). Do đó, \(P\left( F \right) = \frac{{10}}{{36}} = \frac{5}{{18}}\).

Các bài tập cùng chuyên đề
Bài 1 :
Cho hai túi I và II, mỗi túi chứa 3 tấm thẻ được ghi các số 2; 3; 7. Rút ngẫu nhiên từ mỗi túi ra một tấm thẻ và ghép thành số có hai chữ số với tấm thẻ rút từ túi I là chữ số hàng chục. Tính xác suất của các biến cố sau:
a) A: “Số tạo thành chia hết cho 4”.
b) B: “Số tạo thành là số nguyên tố”.
Bài 2 :
Trở lại Ví dụ 3, tính xác suất để cây con có hạt vàng và nhăn.
Bài 3 :
Chọn ngẫu nhiên một gia đình có hai con. Giả thiết rằng biến cố “Sinh con trai” và biến cố “Sinh con gái” là đồng khả năng. Tính xác suất của các biến cố sau:
a) A: “Gia đình đó có cả con trai và con gái”;
b) B: “Gia đình đó có con trai”.
Bài 4 :
Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau:
E: “Có đúng một con xúc xắc xuất hiện mặt 6 chấm”;
F: “Có ít nhất một con xúc xắc xuất hiện mặt 6 chấm”;
G: “Tích của hai chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 6”.
Bài 5 :
Bạn An gieo một đồng xu cân đối và bạn Bình rút ngẫu nhiên một tấm thẻ từ hộp chứa 5 tấm thẻ ghi các số 1; 2; 3; 4; 5. Tính xác suất của các biến cố sau:
E: “Rút được tấm thẻ ghi số lẻ”;
F: “Rút được tấm thẻ ghi số chẵn và đồng xu xuất hiện mặt sấp”;
G: “Rút được tấm thẻ ghi số 5 hoặc đồng xu xuất hiện mặt ngửa”.
Bài 6 :
Có hai túi I và II mỗi túi chứa 4 tấm thẻ được đánh số 1; 2; 3; 4. Rút ngẫu nhiên từ mỗi túi ra một tấm thẻ và nhân hai số ghi trên hai tấm thẻ với nhau. Tính xác suất của các biến cố sau:
a) A: “Kết quả là một số lẻ”.
b) B: “Kết quả là 1 hoặc một số nguyên tố”.
Bài 7 :
Có hai túi đựng các tấm thẻ. Túi I đựng 4 tấm thẻ ghi các chữ cái TT, TH, HT và HH. Túi II đựng 2 tấm thẻ ghi các chữ cái T và H. Từ mỗi túi rút ngẫu nhiên ra một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái, trong đó thẻ hai chữ cái đặt trước, chẳng hạn tấm thẻ TT ghép với tấm thẻ H được ba chữ cái TTH. Tính xác suất của các biến cố sau:
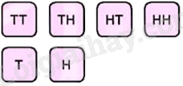
a) E: “Trong ba chữ cái, có hai chữ H và một chữ T”;
b) F: “Trong ba chữ cái, có nhiều nhất hai chữ T”.
Bài 8 :
Gieo đồng thời hai con xúc xắc cân đối và đồng chất I và II. Tính xác suất của các biến cố sau:
G: “Không có con xúc xắc xuất hiện mặt 6 chấm”;
H: “Số chấm xuất hiện trên con xúc xắc I là số lẻ và số chấm xuất hiện trên con xúc xắc II lớn hơn 4”;
K: “Số chấm xuất hiện trên cả hai con xúc xắc lớn hơn 2”.
Bài 9 :
Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất để “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là
A. \(\frac{7}{{36}}\).
B. \(\frac{2}{9}\).
C. \(\frac{1}{6}\).
D. \(\frac{5}{{36}}\).
Bài 10 :
Có hai túi I và II. Túi I chứa 4 tấm thẻ, đánh số 1; 2; 3; 4. Túi II chứa 5 tấm thẻ, đánh số 1; 2; 3; 4; 5. Rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II. Xác suất để hai tấm thẻ rút ra đều ghi số chẵn là
A. \(\frac{1}{5}\).
B. \(\frac{3}{{20}}\).
C. \(\frac{1}{4}\).
D. \(\frac{4}{{21}}\).
Bài 11 :
Một túi đựng 4 viên bi có cùng khối lượng và kích thước, được đánh số 1; 2; 3; 4. Lấy ngẫu nhiên hai viên bi từ trong túi. Xác suất để tích hai số ghi trên hai viên bi lớn hơn 3 là
A. \(\frac{5}{7}\).
B. \(\frac{2}{3}\).
C. \(\frac{3}{4}\).
D. \(\frac{5}{6}\).
Bài 12 :
Có hai túi I và II. Túi I chứa 3 tấm thẻ, đánh số 2; 3; 4. Túi II chứa 2 tấm thẻ, đánh số 5; 6. Từ mỗi túi I và II, rút ngẫu nhiên một tấm thẻ. Tính xác suất của các biến cố sau:
A: “Hai số ghi trên thẻ chênh lệch nhau 2 đơn vị”;
B: “Hai số ghi trên thẻ chênh lệch nhau lớn hơn 2 đơn vị”;
C: “Tích hai số ghi trên hai tấm thẻ là một số chẵn”;
D: “Tổng hai số ghi trên hai tấm thẻ là một số nguyên tố”.
Bài 13 :
Hai bạn Minh và Huy chơi một trò chơi như sau: Minh chọn ngẫu nhiên một số trong tập hợp {5; 6; 7; 8; 9; 10}; Huy chọn ngẫu nhiên một số trong tập hợp {4; 5; 7; 8; 9; 11}. Bạn nào chọn được số lớn hơn thì sẽ là người thắng cuộc. Nếu hai số được chọn bằng nhau thì kết quả là hòa. Tính xác suất của các biến cố sau:
a) A: “Bạn Minh thắng”;
b) B: “Bạn Huy thắng”.
Bài 14 :
Một hộp chứa 4 tấm thẻ cùng loại được đánh số 1; 4; 7; 9. Bạn Khuê và bạn Hương lần lượt mỗi người lấy ra 1 tấm thẻ từ hộp. Tính xác suất của mỗi biến cố sau:
A: “Tích các số ghi trên 2 tấm thẻ là số lẻ”;
B: “Tổng các số ghi trên 2 tấm thẻ là số lẻ”;
C: “Số ghi trên tấm thẻ của bạn Khuê nhỏ hơn số ghi trên tấm thẻ của bạn Hương”.
Bài 15 :
Bạn Thắng có n tấm thẻ cùng loại được đánh số từ 1 đến n. Bạn Thắng rút ngẫu nhiên 1 tấm thẻ. Biết rằng xác suất của biến cố “Lấy được tấm thẻ ghi số có một chữ số là 0,18. Hỏi bạn Thắng có bao nhiêu tấm thẻ?
Bài 16 :
Gieo hai con xúc xắc cân đối và đồng chất. Xét hai biến cố sau:
A: “Xuất hiện hai mặt có cùng số chấm”;
B: “Tổng số chấm trên hai con xúc xắc lớn hơn 8”.
Biến cố nào có khả năng xảy ra cao hơn?
Bài 17 :
Một chiếc hộp có chứa 5 tấm thẻ cùng loại, được đánh số lần lượt là 3; 5; 6; 7; 9.
Lấy ngẫu nhiên đồng thời 2 tấm thẻ từ hộp.
a) Xác định không gian mẫu và số kết quả có thể xảy ra của phép thử.
b) Tính xác suất của mỗi biến cố sau:
A: “Tích các số ghi trên 2 tấm thẻ chia hết cho 3”;
B: “Tổng các số ghi trên 2 tấm thẻ lớn hơn 13”.
Bài 18 :
Một chiếc hộp chứa 1 viên bi xanh, 1 viên bi đỏ và 1 viên bi trắng. Các viên bi có cùng kích thước và khối lượng. Dung lần lượt lấy ra ngẫu nhiên từng viên bi từ trong hộp cho đến khi hết bi.
a) Xác định không gian mẫu của phép thử.
b) Tính xác suất của mỗi biến cố sau:
A: “Viên bi màu xanh được lấy ra cuối cùng”;
B: “Viên bi màu trắng được lấy ra trước viên bi màu đỏ”;
C: “Viên bi lấy ra đầu tiên không phải là bi màu trắng”.
Bài 19 :
Một túi chứa 3 viên bi màu xanh và một số viên bi màu đỏ có cùng kích thước và khối lượng. Bạn Luân lấy ra ngẫu nhiên 1 viên bi. Biết rằng xác suất của biến cố “Lấy được viên bi màu xanh” là 0,6. Hỏi trong túi có tổng bao nhiêu viên bi?
Bài 20 :
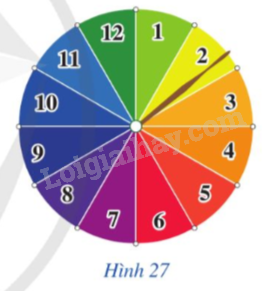
Trong Hoạt động 2, tính xác suất của biến cố D: “Chiếc kim chỉ vào hình quạt ghi số nguyên tố”.
Bài 21 :
Nền ẩm thực Việt Nam được đánh giá cao trên thế giới, thu hút nhiều người sành ăn trong nước và quốc tế. 16 món ngon đặc sắc đến từ các tỉnh, thành phố được chọn ra như sau: phở Thìn (Hà Nội), bánh đa kế (Bắc Ninh), bánh đậu xanh (Hải Dương), bún cá cay (Hải Phòng), gà đồi Yên Thế (Bắc Giang), nộm da trâu (Sơn la), thắng cố (Lào Cai), miến lươn (Nghệ An), cơm hến (Huế), cá mực nhảy (Hà Tĩnh), bánh mì Hội An (Quảng Nam), sủi cảo (TP Hồ Chí Minh), bánh canh Trảng Bàng (Tây Ninh), cá lóc nướng (Cần Thơ), cơm dừa (Bến Tre), gỏi cá (Kiên Giang).
Chọn ngẫu nhiên một món trong 16 món ngon đó. Tính xác suất của mỗi biến cố sau:
a) S: “Món ngon được chọn thuộc miền Bắc”
b) T: “Món ngon được chọn thuộc miền Trung”.
c) U: “Món ngon được chọn thuộc miền Nam”.
Bài 22 :
Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, …, 52, hai thẻ khác nhau thì viết hai số khác nhau.
Rút ngẫu nhiên một thẻ trong hộp, tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 27”.
b) “Số xuất hiện trên thẻ được lấy ra lớn hơn 19 và nhỏ hơn 51”.
Bài 23 :
Một hộp có 25 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 2, 4, 6,…, 48, 50; hai thẻ khác nhau thì viết hai số khác nhau.
Rút ngẫu nhiên một thẻ trong hộp, tính xác suất của biến cố: “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 26” là:
A. \(\frac{{14}}{{25}}\)
B. \(\frac{{13}}{{25}}\)
C. \(\frac{{12}}{{25}}\)
D. \(\frac{{24}}{{25}}\)
Bài 24 :
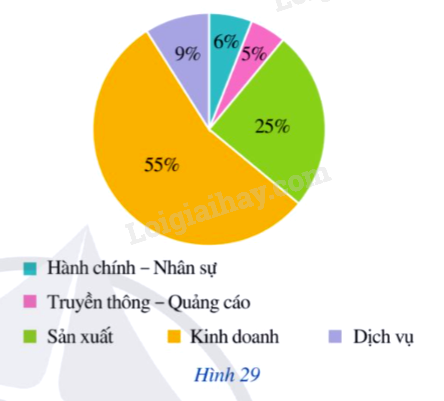
Mỗi nhân viên của một công ty làm việc ở một trong 5 bộ phận của công ty đó là: Hành chính – Nhân sự; Truyền thông – Quảng cáo; Kinh doanh; Sản xuất; Dịch vụ.
Biểu đồ hình quạt tròn Hình 29 thống kê tỉ lệ nhân viên thuộc mỗi bộ phận.
Chọn ngẫu nhiên một nhân viên của công ty, tính xác suất của mỗi biến cố sau:
A: “Nhân viên được chọn thuộc bộ phận Kinh doanh”
B: “Nhân viên được chọn thuộc bộ phận Hành chính – Nhân sự hay Dịch vụ”.
Bài 25 :
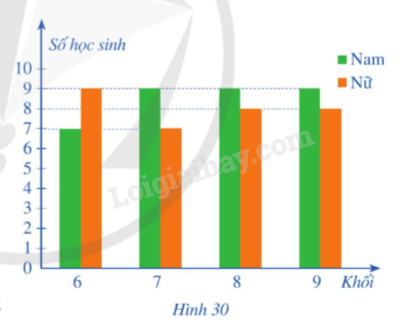
Biểu đồ cột kép ở Hình 30 biểu diễn số lượng học sinh tham gia thi giải thi đấu thể thao của một trường THCS.
Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó.
Tính xác suất của mỗi biến cố sau:
A: “Học sinh được chọn là nam”.
B: “Học sinh được chọn thuộc khối 6”.
C: “Học sinh được chọn là nữ và không thuộc khối 9”.
Bài 26 :
Trong một kì thi học sinh giỏi toán, tỉ lệ học sinh đạt giải là 35%. Chọn ngẫu nhiên một học sinh đã tham gia kì thi đó. Tính xác suất của biến cố: “Học sinh được chọn đạt giải”.
Bài 27 :
Xét phép thử quay bánh xe và quan sát xem khi nó dừng thì mũi kim (được gắn cố định) chỉ vào ô số mấy. Tính xác suất của các biến cố:
a) X: “Kim chỉ ô số lẻ”;
b) Y: “Kim chỉ ô có số là bội của 4”;
c) Z: “Kim chỉ ô số là ước lớn hơn 1 của 18”.
Bài 28 :
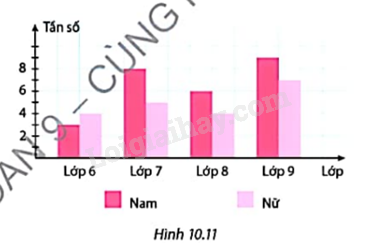
Hình 10.11 là biểu đồ thống kê số học sinh tham gia câu lạc bộ cờ vua. Lấy ngẫu nhiên một học sinh trong số này. Tính xác suất của các biến cố:
a) Lấy được một học sinh nữ lớp 9;
b) Lấy được một học sinh lớp 6;
c) Lấy được một học sinh nam lớp 7 hoặc lớp 8.
Bài 29 :
Trở lại với tình huống ở phần Khởi động. Hãy tính xác suất của biến cố “Bạn Trung được điểm thưởng “ trong mỗi lần rút thẻ.
Hoạt động khởi động: Trò chơi “rút thẻ” : Trong hộp có 10 thẻ giống hệt nhau. Trên mỗi thẻ có ghi một trong các số từ 1 đến 10 (không có thẻ nào trùng số). Bạn Trung rút ngẫu nhiên một thẻ, xác định số ghi trên thẻ rồi bỏ lại vào hộp. Nếu lấy được thẻ có ghi một số chia hết cho 3 thì Trung được 1 điểm thưởng và có quyền rút thẻ lần nữa. Nếu rút được thẻ ghi số không chia hết cho 3 thì Trung phải nhường lượt chơi cho đối thủ. Kết thúc trò chơi, ai nhiều điểm hơn thì người đó thắng.
Bài 30 :
Chuẩn bị cho ngày Hội xuân được tổ chức hằng năm, khối 9 chịu trách nhiệm tổ chức một số gian hàng và trò chơi. Khối 9 của trường có 16 lớp nên ban tổ chức chuẩn bị 16 phiếu để các lớp bốc thăm. Các phiếu được đánh số thứ tự từ 1 đến 16 và trên đó có ghi một trong ba nhiệm vụ “tổ chức gian hàng ẩm thực”, “tổ chức gian hàng quà lưu niệm”, “tổ chức trò chơi dân gian”. Biết rằng trường dự định tổ chức 7 gian “ẩm thực” và số gian “trò chơi dân gian” nhiều gấp hai lần số gian “quà lưu niệm”.
Lớp 9A1 được mời lên bốc thăm đầu tiên. Tính xác suất để lớp 9A1 bốc được phiếu “tổ chức trò chơi dân gian”.


















Danh sách bình luận