Đề bài

Tích của hai số tự nhiên bằng \(105.\) Có bao nhiêu cặp số thỏa mãn?

• A. $4$                 
• B. $6$                      
• C. $10$                         
• D. $8$

Phương pháp giải

+ Phân tích số \(105\) ra thừa số nguyên tố.

+ Tìm các ước của \(105.\) Các số \(a;b\) chính là các ước của \(105\) sao cho tích của chúng bằng \(105.\)

Lời giải của GV Loigiaihay.com

Gọi hai số tự nhiên cần tìm là \(a\) và \(b\left( {a;b \in N} \right)\)

Ta có \(a.b = 105\)

Phân tích số \(105\) ra thừa số nguyên tố ta được \(105 = 3.5.7\)

Vì vậy ta có các giá trị a có thể là:

1; 3; 5; 7;

3.5 = 15; 3.7 = 21; 5.7 = 35;

3.5.7 = 105.

Các số \(a;b\) là ước của \(105\) , do đó ta có bảng sau:

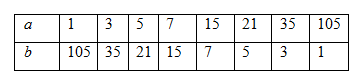
Vậy có \(8\) cặp số thỏa mãn yêu cầu.

Đáp án : D