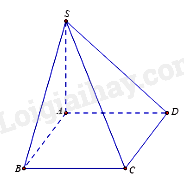
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,SA vuông góc với đáy, \(SA = a\). Khoảng cách giữa hai đường thẳng SB và CD là
-
A.
\(a\).
-
B.
2a.
-
C.
\(a\sqrt 2 \).
-
D.
\(a\sqrt 3 \).
Vì \(DC\parallel AB\) nên \(d(SB;CD) = d(CD;(SAB)) = d(D;(SAB)) = AD = a\)
Đáp án A.
Đáp án : A
Các bài tập cùng chuyên đề
Với b,c là hai số thực dương tùy ý thỏa mãn \({\rm{lo}}{{\rm{g}}_5}b \ge {\rm{lo}}{{\rm{g}}_5}c\), khẳng định nào dưới đây là đúng?
Đạo hàm của hàm số \(y = {2^x}\) là:
Nghiệm của phương trình \({2^x} = 3\) là
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh \(a,{\mkern 1mu} {\mkern 1mu} AA' \bot \left( {ABCD} \right)\) và \(AA' = 3a.\) Thể tích của khối lăng trụ đã cho bằng
Cho hình lập phương \(ABCD \cdot A'B'C'D'\) có cạnh bằng \(a\) (tham khảo hình vẽ).
Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( {BDA'} \right)\) và \(\left( {ABCD} \right)\). Giá trị của \({\rm{sin}}\varphi \) bằng
Hệ số góc tiếp tuyến của đồ thị hàm số \(y = 2{x^2} - 2\) tại điểm có hoành độ \({x_0} = 2\)là:
Có hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,6. Xác suất để có ít nhất một người bắn trúng là:
Tính đạo hàm của hàm số sau \(y = \frac{{ - 3x + 4}}{{x - 2}}\).
Cho hình chóp \(S.ABC,{\mkern 1mu} SA\) vuông góc với đáy, \(J\) là hình chiếu của \(A\) trên BC. Khẳng định nào sau đây là đúng?
Có ba chiếc hộp: hộp I có 4 bi đỏ và 5 bi xanh, hộp II có 3 bi đỏ và 2 bi đen, hộp III có 5 bi đỏ và 3 bi vàng. Lấy ngẫu nhiên ra một hộp rồi lấy một viên bi từ hộp đó. Xác suất để viên bi lấy được màu đỏ bằng
Tập nghiệm của bất phương trình \({\rm{lo}}{{\rm{g}}_7}\left( {5x - 2} \right) > {\rm{lo}}{{\rm{g}}_7}\left( {6 - 3x} \right)\) là
Tập nghiệm của bất phương trình \({5^{x + 2}} < {\left( {\frac{1}{{25}}} \right)^{ - x}}\) là
Hàm số \(y = \left( {1 + x} \right)\sqrt {1 - x} \)có đạo hàm \(y' = \frac{{ax + b}}{{2\sqrt {1 - x} }}\). Tính \(a + b.\)
Tìm tất cả các giá trị của tham số \(m\) để phương trình \({9^x} - {2.6^x} + m{.4^x} = 0\) có hai nghiệm trái dấu.
Cho chuyển động thẳng xác định bởi phương trình \(S = {\rm{\;}} - {t^3} + 3{t^2} + 9t\), trong đó \(t\) tính bằng giây và \(S\) tính bằng mét. Tính vận tốc của chuyển động tại thời điểm gia tốc triệt tiêu.
Tính tổng tất cả các nghiệm nguyên của bất phương trình \(\log \left( {{x^2} + 2x + 3} \right) \le \log 6\)
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, \(AB = a\sqrt 3 \), AC = AA’ = a. Giá trị sin của góc giữa đường thẳng AC’ và mặt phẳng (BCC’B’) bằng
Một lớp có 60 sinh viên trong đó 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một sinh viên. Tính xác suất của các biến cố sinh viên được chọn không học tiếng Anh và tiếng Pháp.
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng \(\left( {A'BC} \right)\) tạo với đáy một góc bằng \({60^\circ }.\) Thể tích khối lăng trụ ABC.A'B'C' bằng:
Cho hàm số \(f\left( x \right) = {x^3} - 2{x^2} + 4\) có đồ thị \(\left( C \right)\). Tìm hoành độ tiếp điểm của đồ thị \(\left( C \right)\) biết tiếp tuyến có hệ số góc bằng \( - 1\).
