Đề bài

Cho tam giác ABC có AB = AC. Trên các cạnh AB và AC lấy các điểm D, E sao cho \(AD = AE\). Gọi K là giao điểm của BE và CD. Chọn câu sai

• A. BE = CD.
• B. BK = KC.
• C. BD = CE.
• D. DK = KC.

Phương pháp giải

Chứng minh các \(\Delta ABE = \Delta ACD\) và \(\Delta BKC\) cân để kiểm tra.

Lời giải của GV Loigiaihay.com

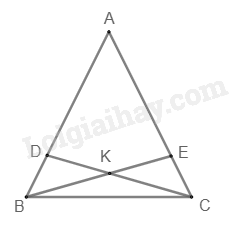
Xét tam giác ABE và ACD có:

AB = AC (gt)

\(\widehat {BAC}\) chung

AE = AD (gt)

suy ra \(\Delta ABE = \Delta ACD\left( {c.g.c} \right)\)

suy ra BE = CD (hai cạnh tương ứng nên A đúng.

và \(\widehat {ABE} = \widehat {ACD}\) (hai góc tương ứng)

Mà \(\widehat {ABC} = \widehat {ACB}\) (tam giác ABC cân tại A vì AB = AC)

Suy ra \(\widehat {KBC} = \widehat {KCB}\) nên \(\Delta BKC\) cân tại K.

Do đó BK = CK nên B đúng.

Vì AB = AC, AD = AE nên AB – AD = AC – AE hay BD = CE nên C đúng.

Ta chưa đủ điều kiện có DK = KC nên đáp án D sai.

Đáp án D.

Đáp án : D