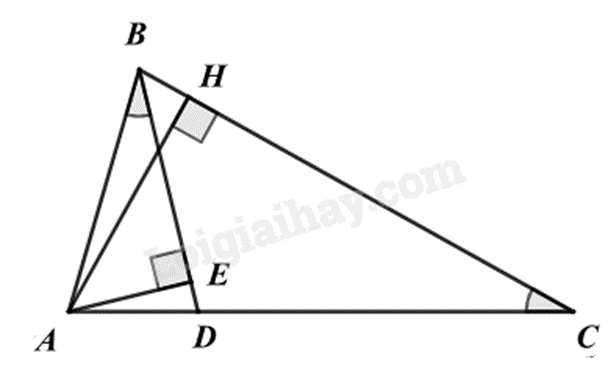
Cho \(\Delta ABC\) vuông tại A có \(AB = 6cm\) và \(AC = 8cm\). Đường phân giác của góc ABC cắt AC tại D. Từ C kẻ \(CE \bot BD\) kẻ E.
a) Tính độ dài BC và tỉ số \(\frac{{AD}}{{DC}}\).
b) Chứng minh $\Delta ABD\backsim \Delta EBC$. Từ đó suy ra \(BD.EC = AD.BC\).
c) Chứng minh \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}\).
d) Gọi EH là đường cao của \(\Delta EBC\). Chứng minh \(CH.CB = ED.EB\).
a) Sử dụng định lí Pythagore để tính BC, sử dụng tính chất tia phân giác để tính \(\frac{{AD}}{{DC}}\).
b) Chứng minh $\Delta ABD\backsim \Delta EBC$ theo trường hợp góc – góc suy ra tỉ số các cạnh tương ứng.
c) Chứng minh \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}} = \frac{{AD}}{{AB}}\)
d) Chứng minh \(CH.CB = ED.EB = C{E^2}\)
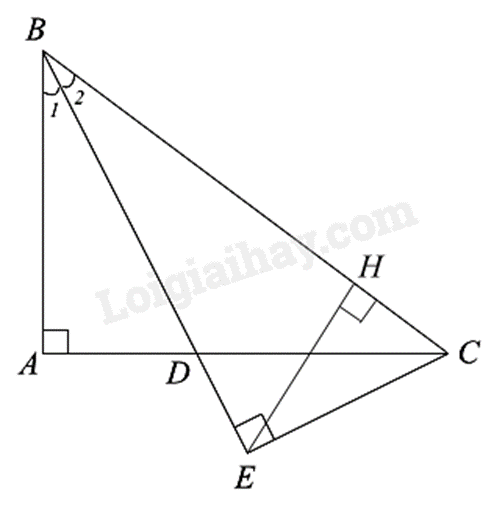
a) Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông tại A, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\)
Suy ra \(BC = \sqrt {100} = 10\) (cm).
Vì BD là tia phân giác của góc ABC nên ta có:
\(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\)
b) Theo đề bài, \(CE \bot BD\) tại E nên \(\widehat {BEC} = {90^0}\)
Xét \(\Delta ABD\) và \(\Delta EBC\) có:
\(\widehat {BAD} = \widehat {BEC} = {90^0}\)
\(\widehat {{B_1}} = \widehat {{B_2}}\) (BD là tia phân giác của góc ABC)
Suy ra $\Delta ABD\backsim \Delta EBC$ (g.g) (đpcm)
Suy ra \(\frac{{BD}}{{AD}} = \frac{{BC}}{{EC}}\) (tỉ số các cạnh tương ứng)
Do đó \(BD.EC = AD.BC\) (đpcm)
c) Vì \(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}}\) nên \(\frac{{CD}}{{BC}} = \frac{{AD}}{{AB}}\) (1)
Vì $\Delta ABD\backsim \Delta EBC$ (cmt) nên \(\frac{{AD}}{{EC}} = \frac{{AB}}{{EB}}\) suy ra \(\frac{{AD}}{{AB}} = \frac{{EC}}{{EB}}\) (2)
Từ (1) và (2) suy ra \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}\) (đpcm)
d) Xét \(\Delta CHE\) và \(\Delta CEB\) có:
\(\widehat {CHE} = \widehat {CEB} = {90^0}\)
\(\widehat C\) chung
Suy ra $\Delta CHE\backsim \Delta CEB$ (g.g) nên \(\frac{{CH}}{{CE}} = \frac{{CE}}{{CB}}\) suy ra \(CH.CB = C{E^2}\) (3)
Tương tự, $\Delta CDE\backsim \Delta BCE$ (g.g) nên \(\frac{{ED}}{{EC}} = \frac{{CE}}{{BE}}\) suy ra \(ED.EB = C{E^2}\)(4)
Từ (3) và (4) suy ra \(CH.CB = ED.EB\) (đpcm)

Các bài tập cùng chuyên đề
Bài 1 :
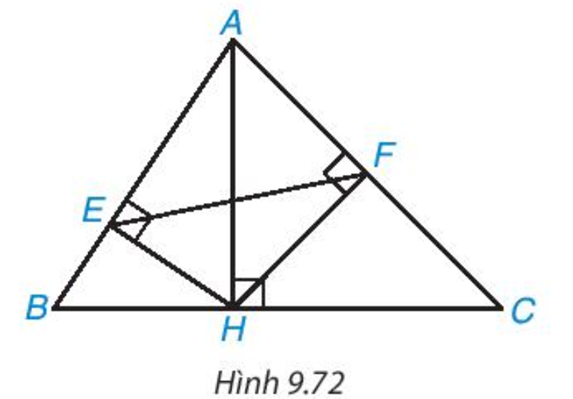
Trong hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng
a) ΔAEH ∽ ΔAHB
b) ΔAFH ∽ ΔAHC
c) ΔAFE ∽ ΔABC
Bài 2 :
Cho tam giác ABC vuông tại A có AB=5cm, AC=4cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB
a) Chứng minh rằng ΔHDA ∽ ΔAHC
b) Tính độ dài các đoạn thẳng HA, HB, HC, HD
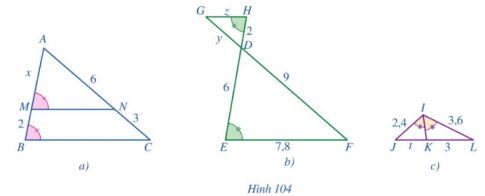
Bài 3 :
Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c.
Bài 4 :
Tính độ dài \(AF\) và \(EF\) trong Hình 6.112.

Bài 5 :
Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:
a) \(HA.HD = HB.HE = HC.HF\);
b) $\Delta AFC\backsim \Delta AEB$ và $AF.AB=AE.AC\,;$
c) $\Delta BDF\backsim \Delta EDC$ và DA là tia phân giác của góc EDF.
Bài 6 :
Cho tam giác nhọn ABC có các đường cao AD, BE, CF. Chứng minh rằng:
a) $\Delta BDF\backsim \Delta BAC$ và $\Delta CDE\backsim \Delta CAB$;
b) \(BF.BA + CE.CA = B{C^2}\)
Bài 7 :
Cho tam giác ABC vuông tại A có đường cao AH. Cho M là một điểm nằm trên cạnh BC (M nằm giữa C và H). Kẻ đường thẳng qua M vuông góc với BC lần lượt cắt AC và tia đối của tia AB tại N và P. Chứng minh rằng:
a) $\Delta ANP\backsim \Delta HBA$ và $\Delta MCN\backsim \Delta MPB$;
b) \(\frac{{MB}}{{MC}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{PB}} = 1\)
Bài 8 :
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh rằng:
a) \(AM.AB = A{H^2}\) và \(AM.AB = AN.AC\)
b) $\Delta AMN\backsim \Delta ACB$
Bài 9 :
Cho ABC và A’B’C’ lần lượt là các tam giác vuông tại đỉnh A và A’. Gọi M, M’ lần lượt là trung điểm của AC và A’C’. Chứng minh rằng:
a) \(B{C^2} + 3B{A^2} = 4B{M^2}\) và \(B'C{'^2} + 3B'A{'^2} = 4B'M{'^2}\);
b) Nếu \(\frac{{BC}}{{BM}} = \frac{{B'C'}}{{B'M'}}\) thì $\Delta ABC\backsim \Delta A'B'C'$.
Bài 10 :
Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN.
a) Chứng minh rằng \(CM \bot DN\).
b) Biết \(AB = 4cm,\) hãy tính diện tích tam giác ONC.
Bài 11 :
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N, P lần lượt là trung điểm của HA, HB, HC. Chứng minh rằng:
a) $\Delta MNP\backsim \Delta ABC$ và tìm tỉ số đồng dạng
b) $\Delta ABN\backsim \Delta CAM$ và $\Delta ACP\backsim \Delta BAM$
c) \(AN \bot CM\) và \(AP \bot BM\)
Bài 12 :
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là trung điểm của AH, AB. Chứng minh rằng $\Delta CAM\backsim \Delta CBN$ và $\Delta CHM\backsim \Delta CAN$
Bài 13 :
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB.
a) Chứng minh ΔBMP ∽ ΔMCN
b) Tính độ dài đoạn thẳng AM
Bài 14 :
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M,N lần lượt là các điểm trên các đoạn thẳng AB, AH sao cho AM = 2.MB, AN = $\frac{1}{2}$NH.
Chứng minh rằng $\Delta CAN\backsim \Delta CBM$ và $\Delta CHN\backsim \Delta CAM$.
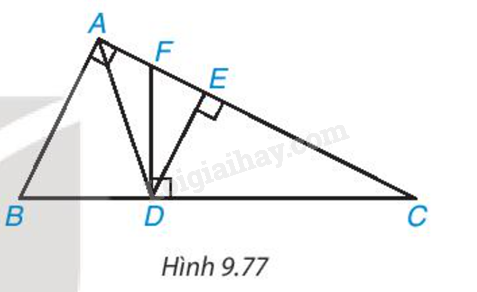
Bài 15 :
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC. Chứng minh rằng:
a) \(\frac{B\text{D}}{BC}=\frac{AB}{AB+AC}\), từ đó suy ra \(A\text{E}=\frac{AB.AC}{AB+AC}\);
b) ΔDFC ∽ ΔABC;
c) DF = DB
Bài 16 :
Cho tam giác ABC có \(AB = 3cm,AC = 4cm,BC = 5cm.\) Lấy điểm D trên cạnh BC sao cho \(BD = 2cm.\) Lấy các điểm E, F trên các cạnh AB, AC sao cho DE, DF lần lượt vuông góc với AB, AC.
a) Chứng minh rằng $\Delta BDE\backsim \Delta DCF$
b) Tính độ dài đoạn thẳng AD.
Bài 17 :
Cho \(\Delta ABC\) có AB = 9cm, AC = 12cm, BC = 15cm. Trên cạnh AC lấy điểm D sao cho CD = 4cm, trên cạnh BC lấy điểm M sao cho BM = 10cm. Kẻ đoạn thẳng MD.
a) Chứng tỏ rằng DM // AB.
b) Chứng minh $\Delta BAC\backsim \Delta MDC$.
c) Xác định tỉ số giữa diện tích của tam giác MDC với diện tích tam giác ABC.
Bài 18 :
Cho \(\Delta ABC\) có AB = 2cm, AC = 4cm. Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\). Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\).
a) $\Delta ABD\backsim \Delta ACB$.
b) \(\widehat {ADB} = \widehat {ABC}\).
c) \(AD = 0,5cm,DC = 3,5cm\).
d) \({S_{\Delta ABH}} = 4{S_{\Delta ADE}}\).
Bài 19 :
Cho tam giác ABC (AB < AC) vuông tại A có đường cao AH.
a) Chứng minh rằng $\Delta ABC\backsim \Delta HAC$.
b) Lấy điểm I thuộc đoạn AH (I không trùng với A, H). Qua B kẻ đường thẳng vuông góc với CI tại K. Chứng minh rằng \(CH.CB = CI.CK\).
c) Tia BK cắt tia HA tại điểm D. Chứng minh \(CH.CB + DK.DB = C{D^2}\).
Bài 20 :
Cho hình chữ nhật ABCD. Kẻ \(AH \bot BD\) tại H.
a) Chứng minh rằng $\Delta ABD\backsim \Delta HBA$.
b) Chứng minh rằng \(B{C^2} = BD.DH\).
c) Kẻ DE là đường phân giác của tam giác ABD. Gọi I là giao điểm của DE và AH. Chứng minh \(\Delta AIE\) cân và \(A{E^2} = IH.EB\).
Bài 21 :
Cho tam giác ABC cân tại A có đường cao AM, N là trung điểm của AC. Kẻ Ax // BC, cắt MN tại E.
a) M là trung điểm của BC.
b) ME // AB.
c) AE = MC.
d) $\Delta AEN\backsim \Delta CNM$.
Bài 22 :
Cho hình vuông ABCD cạnh a, điểm E thuộc cạnh BC, điểm F thuộc cạnh AD sao cho CE = AF. Các đường thẳng AE, BF cắt đường thẳng CD theo thứ tự ở M và N.
1. Chứng minh \(CM.DN=a^2\)
2. Gọi K là giao điểm của NA và MB. Chứng minh \(\widehat{MKN}=90^\circ\).


















Danh sách bình luận