Cho \(\Delta MNP\) có MN = 8cm, MP = 16cm. Điểm D thuộc cạnh MN sao cho ND = 2cm, điểm E thuộc cạnh MP sao cho EP = 13cm. Khi đó \(\Delta MNP\) đồng dạng với tam giác nào?
-
A.
\(\Delta MED\).
-
B.
\(\Delta MDE\).
-
C.
\(\Delta DEM\).
-
D.
\(\Delta DME\).
Dựa vào các trường hợp đồng dạng của hai tam giác.
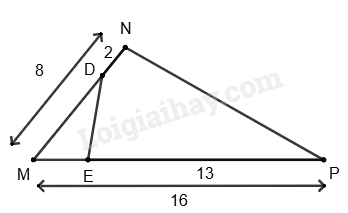
Ta có:
MD = MN – ND = 8 – 2 = 6(cm)
ME = MP – PE = 16 – 13 = 3(cm)
Xét \(\Delta MNP\) và \(\Delta MED\) có:
\(\widehat M\) chung
\(\frac{{ME}}{{MD}} = \frac{{MN}}{{MP}} = \frac{1}{2}\)
Suy ra $\Delta MNP\backsim \Delta MED$ (c.g.c)
Đáp án A.
Đáp án : A
Các bài tập cùng chuyên đề
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
Phương trình \(2x + 7 = 3x + 15\) có tập nghiệm là
Cho $\Delta ABC\backsim \Delta DEF$ có \(\frac{{AB}}{{DE}} = \frac{1}{2}\) và diện tích \(\Delta DEF\) bằng \(160c{m^2}\). Khi đó diện tích \(\Delta ABC\) bằng:
Giải các phương trình sau:
a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)
c) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\)
Cho \(\Delta ABC\) có \(AB = 2cm,AC = 4cm\). Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\).
a) Chứng minh $\Delta ABD\backsim \Delta ACB$
b) Tính AD và DC.
c) Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\). Chứng minh rằng diện tích \(\Delta ABH\) gấp 4 lần diện tích \(\Delta ADE\).
