Cho tam giác ABC vuông tại A, đường cao AH. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng?
(1) \(A{B^2} = BH.CH\)
(2) \(A{C^2} = CH.BC\)
(3) \(B{C^2} = AB.AC\)
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
Xác định các tam giác đồng dạng suy ra tỉ số đồng dạng giữa các cạnh.
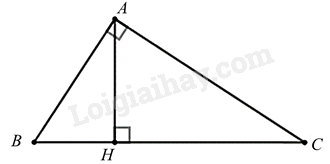
Ta có:
$\Delta ABC\backsim \Delta HBA\left( g.g \right)\Rightarrow \frac{AB}{BC}=\frac{BH}{AB}\Rightarrow A{{B}^{2}}=BH.BC$ nên khẳng định (1) sai.
$\Delta ABC\backsim \Delta HAC\left( g.g \right)\Rightarrow \frac{AC}{BC}=\frac{CH}{AC}\Rightarrow A{{C}^{2}}=CH.BC$ nên khẳng định (2) đúng.
Khẳng định (3) sai.
Vậy chỉ có 1 khẳng định đúng (khẳng định (2)).
Đáp án B.
Đáp án : B
Các bài tập cùng chuyên đề
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Phương trình \(3x + m - x - 1 = 0\) nhận \(x = - 3\) là nghiệm thì m là:
Một ô tô đi từ A đến B từ 6 giờ sáng, lúc 7 giờ sáng cùng ngày, một xe khách cũng đi từ A và tới B cùng lúc với ô tô. Vậy nếu gọi thời gian đi của xe khách là x ( giờ) thì thời gian đi của ô tô là:
Cho hàm số \(y = f\left( x \right) = 2x + 1\), điểm nào sau đây thuộc đồ thị hàm số
Giá trị m để đường thẳng \(y = mx - 4\) cắt đường thẳng \(y = 2x - 1\) tại điểm có hoành độ bằng 2 là:
Một túi đựng các viên kẹo giống hệt nhau, chỉ khác màu nhau, trong đó có 6 viên kẹo màu cam, 3 viên kẹo màu đỏ, 7 viên kẹo màu trắng. An lấy ngẫu nhiên một viên kẹo trong túi. Tính xác suất lấy được viên kẹo màu cam.
Một cửa hàng thống kê số lượng các loại điện thoại bán được trong một năm vừa qua như sau:
Tính xác suất thực nghiệm của biến cố E: “Chiếc điện thoại loại A được bán năm đó của của hàng”.
Cho hình bình hành ABCD, kẻ \(AH \bot CD\) tại H; \(AK \bot BC\) tại K. Chọn câu trả lời đúng.
Hình biểu diễn đúng tâm phối cảnh của cặp hình đồng dạng này là:
Hình chóp tam giác đều có bao nhiêu mặt?
Một chậu cây cảnh mini có hình dạng là một hình chóp tứ giác đều có chiều cao bằng 35cm, cạnh đáy bằng 24cm . Độ dài trung đoạn của chậu cây cảnh là
1. Giải các phương trình sau:
a) \(2\left( {x - 3} \right) = 5\left( {x - 2} \right) + 8\)
b) \(\frac{{x - 1}}{9} + \frac{{x - 3}}{7} = 2\)
2. Cho hàm số \(y = - 2x + 5\) có đồ thị (d).
a) Trên mặt phẳng tọa độ Oxy, vẽ đồ thị (d). Gọi A, B lần lượt là giao điểm của (d) với các trục tọa độ Ox, Oy. Tính diện tích tam giác OAB.
b) Viết phương trình đường thẳng (d’) qua \(M\left( {1;5} \right)\) và song song với (d).
Giải bài toán bằng cách lập phương trình
Tổ sản xuất được giao dệt một số thảm trong 20 ngày. Nhưng do tổ tăng năng suất 20% nên đã hoàn thành sau 18 ngày. Không những vậy mà tổ còn làm thêm được 24 chiếc thảm. Tính số thảm thực tế tổ sản xuất làm được.
Một cuốn lịch để bàn có hình dạng là một hình chóp tam giác đều có các mặt là các tam giác đều có cạnh bằng 20cm. Tính thể tích của cuốn lịch. (làm tròn đến chữ số thập phân thứ hai).
Cho \(\Delta ABC\) có ba góc nhọn (AB < AC). Kẻ đường cao AH, từ H kẻ HD và HE lần lượt vuông góc với AB và AC (\(D \in AB,E \in AC\)).
a) Chứng minh $\Delta AHD\backsim \Delta ABH$.
b) Chứng minh AD.AB = AE.AC.
c) Gọi I là trung điểm của HC. Điểm F là chân đường vuông góc hạ từ I đến AC.
Chứng minh \(C{A^2} - H{C^2} = A{F^2} - C{F^2}\)
Ở một trang trại nuôi chim cút, người ta nhận thấy xác suất một quả trứng cút có cân nặng dưới 9g là 0,5. Hãy ước lượng xem trong một lô 3000 quả trứng cút của trang trại có khoảng bao nhiêu quà trứng có cân nặng dưới 9g.
