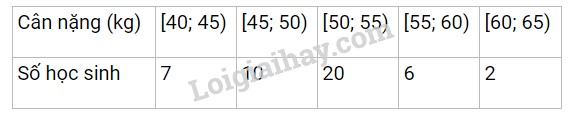
Cho mẫu số liệu về cân nặng (kg) của 45 học sinh lớp 11A được cho bởi bảng sau:
a) Tứ phân vị thứ nhất \({Q_1}\) là 47
b) Trung vị \({M_e}\) là 51,4
c) Tứ phân vị thứ ba \({Q_3}\) là 54,2
d) Mốt \({M_o} = 20\)
a) Tứ phân vị thứ nhất \({Q_1}\) là 47
b) Trung vị \({M_e}\) là 51,4
c) Tứ phân vị thứ ba \({Q_3}\) là 54,2
d) Mốt \({M_o} = 20\)
Sử dụng công thức tính tứ phân vị của mẫu số liệu và Mốt
Cỡ mẫu là n = 7 + 10 + 20 + 6 + 2 = 45
Gọi x1, x2, ….., x45 là cân nặng của 45 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần.
Khi đó, trung vị là x23. Do giá trị x23 thuộc nhóm [50; 55) nên nhóm này chứa trung vị.
Do đó p = 3; a3 = 50, m3 = 20; m1 + m2 = 7 + 10 = 17; a4 – a3 = 55 – 50 = 5
Khi đó
\({M_e} = {a_3} + \frac{{\frac{n}{2} - ({m_1} + {m_2})}}{{{m_3}}}({a_4} - {a_3}) = 50 + \frac{{\frac{{45}}{2} - 17}}{{20}}.5 \approx 51,4\).
Vậy Me = 51,4.
Từ Me = 51,4, suy ra Q2 = 51,4.
- Tứ phân vị thứ nhất Q1 là trung vị của nửa dãy bên trái Q2 nên \({Q_1} = \frac{{{x_{11}} + {x_{12}}}}{2}\)
Do x11 và x12 đều thuộc nhóm [45; 50) nên nhóm này chứa Q1. Do đó, p = 2, a2 = 45, m2 = 10, m1 = 7; a3 – a2 = 5.
Ta có \({Q_1} = {a_2} + \frac{{\frac{n}{4} - {m_1}}}{{{m_2}}}({a_3} - {a_2}) = 45 + \frac{{\frac{{45}}{2} - 7}}{{10}}.5 \approx 47,1\)
- Tứ phân vị thứ ba Q3 là trung vị của nửa dãy bên phải Q2 nên \({Q_3} = \frac{{{x_{34}} + {x_{35}}}}{2}\).
Do x34 và x35 đều thuộc nhóm [50; 55) nên nhóm này chứa Q3. Do đó, p = 3, a3 = 50, m3 = 20, m1 + m2 = 7 + 10 = 17; a4 – a3 = 55 – 50 = 5.
Ta có \({Q_3} = {a_3} + \frac{{\frac{{3n}}{4} - ({m_1} + {m_2})}}{{{m_3}}}({a_4} - {a_3}) = 50 + \frac{{\frac{{3.45}}{4} - 17}}{{20}}.5 \approx 54,2\) .
Vậy tứ phân vị: Q1 ≈ 47,1; Q2 ≈ 51,4; Q3 ≈ 54,2.
- Ta thấy tần số lớn nhất là 20 nên nhóm chứa mốt là nhóm [50; 55).
Ta có j = 3, a3 = 50, m3 = 20, m2 = 10, m4 = 6, h = 55 – 50 = 5
Khi đó
\({M_0} = {a_3} + \frac{{{m_3} - {m_2}}}{{\left( {{m_3} - {m_2}} \right) + \left( {{m_3} - {m_4}} \right)}}h = 50 + \frac{{20 - 10}}{{(20 - 10) + (20 - 6)}}.5 \approx 52,1\)
Vậy Mo ≈ 52,1.
Các bài tập cùng chuyên đề
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\)có nghiệm là
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm\(M( - 2;6).\) Phương trình của (d) là
Tính thời gian trung bình giải bài tập của học sinh lớp 11A được cho trong bảng sau:
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\)là
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm x0 = 1 thì m bằng:
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\)bằng
