Đề bài

Cho lăng trụ tứ giác $ABCD.A'B'C'D'$. Có đáy là hình vuông và cạnh bên bằng $2a$. Hình chiếu của $A'$ trên mặt phẳng $\left( {ABCD} \right)$ là trung điểm của cạnh $AD$, đường thẳng $A'C$ hợp với mặt phẳng $\left( {ABCD} \right)$một góc ${45^o}$.

a) $A'H \bot AC$

Đúng

Sai

b) A’H không vuông góc (BB’C’C)

Đúng

Sai

c) $\left( {A'C,(ABCD)} \right) = \widehat {A'CH}$

Đúng

Sai

d) Thể tích khối lăng trụ bằng $4{a^3}\sqrt 5$

Đúng

Sai

Đáp án

a) $A'H \bot AC$

Đúng

Sai

b) A’H không vuông góc (BB’C’C)

Đúng

Sai

c) $\left( {A'C,(ABCD)} \right) = \widehat {A'CH}$

Đúng

Sai

d) Thể tích khối lăng trụ bằng $4{a^3}\sqrt 5$

Đúng

Sai

Phương pháp giải

Sử dụng định lý đường thẳng vuông góc với mặt phẳng; góc giữa đường thẳng với mặt phẳng

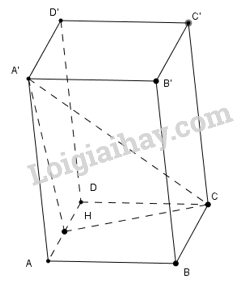
a) $A'H \bot (ABCD) \Rightarrow A'H \bot AC$

b) A’H không vuông góc (BB’C’C)

c)d) Ta có: $A'H \bot (ABCD)$

$\Rightarrow HC$là hình chiếu của $A'C$ trên $\left( {ABCD} \right)$

$\Rightarrow (\widehat {A'C,(ABCD)}) = (\widehat {A'C,HC}) = \widehat {HCA'} = {45^o}$

Áp dụng định lý Pitago cho tam giác HDC vuông tại D ta có:

$HC = \sqrt {H{D^2} + D{C^2}}  = \sqrt {{a^2} + {{\left( {2a} \right)}^2}}  = a\sqrt 5$

$\Rightarrow A'H = HC.\tan {45^o} = a\sqrt 5$

$\Rightarrow {V_{ABCD.A'B'C'D'}} = A'H.{S_{ABCD}} = a\sqrt 5 .{\left( {2a} \right)^2} = 4{a^3}\sqrt 5$.