Đề bài

Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và B, $SA \bot \left( {ABCD} \right)$, $AD = 2a,AB = BC = a$. Chứng minh rằng:

a) Tam giác SBC là tam giác vuông.

b) $CD \bot SC$.

Phương pháp giải

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải của GV Loigiaihay.com

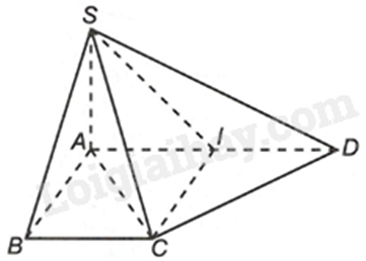
a) Vì $SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC$.

Vì ABCD là hình thang vuông tại A và B nên $AB \bot BC$.

Ta có: $SA \bot BC$, $AB \bot BC$, SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB) nên $BC \bot \left( {SAB} \right)$. Lại có, $SB \subset \left( {SBC} \right) \Rightarrow BC \bot SB$. Suy ra, tam giác SBC vuông tại B.

b) Gọi I là trung điểm của AD. Do đó, $AI = ID = \frac{1}{2}AD = a$

Tứ giác ABCI có: AI//BC (do tứ giác ABCD là hình thang vuông tại A, B), $AI = BC\left( { = a} \right)$ nên tứ giác ABCI là hình bình hành. Lại có: $BC = AB$ nên tứ giác ABCI là hình thoi. Mà $\widehat {BAI} = {90^0}$ nên ABCI là hình vuông. Do đó, $\widehat {AIC} = {90^0} \Rightarrow \widehat {CID} = {90^0}$

Tam giác CID có: $\widehat {CID} = {90^0},CI = ID\left( { = a} \right)$ nên tam giác CID vuông cân tại I.

Suy ra: $\widehat {DCI} = {45^0}$.

Lại có: CA là phân giác góc ICB (do ABCI là hình vuông) nên $\widehat {ACI} = \frac{1}{2}\widehat {ICB} = \frac{1}{2}{.90^0} = {45^0}$

Suy ra: $\widehat {ACD} = \widehat {ACI} + \widehat {ICD} = {90^0}$ hay $AC \bot CD$

Vì $SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \Rightarrow SA \bot DC$

Ta có: $AC \bot CD$, $SA \bot DC$, SA và AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên $DC \bot \left( {SAC} \right)$. Mà $SC \subset \left( {SAC} \right) \Rightarrow CD \bot SC$