Đề bài

Cho hình chóp S. ABCD có đáy ABCD là hình thoi và $SA = SC,{\rm{ }}SB = SD$. Gọi O là giao điểm của AC và BD. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là:

• A. A.
• B. C.
• C. O.
• D. D.

Phương pháp giải

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P).

Lời giải của GV Loigiaihay.com

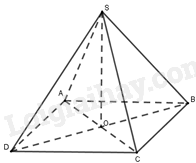
Vì ABCD là hình thoi, O là giao điểm của AC và BD nên O là trung điểm của AC, O là trung điểm của BD.

Vì $SA = SC$ nên tam giác SAC cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác. Suy ra, $SO \bot AC$.

Vì $SB = SD$ nên tam giác SBD cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác. Suy ra, $SO \bot BD$.

Vì $SO \bot AC$, $SO \bot BD$ và BD và AC cắt nhau tại O và nằm trong mặt phẳng (ABCD) nên $SO \bot \left( {ABCD} \right)$. Do đó, hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm O.

Đáp án C.

Đáp án : C