Đề bài

Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Cạnh bên CC’ vuông góc với đáy và $CC' = a$. Gọi M, I lần lượt là trung điểm của BB’, BC.

a) Chứng minh rằng: $AM \bot BC'$.

b) Gọi K là điểm trên đoạn A’B’ sao cho $B'K = \frac{a}{4}$ và J là trung điểm của B’C’. Chứng minh rằng: $AM \bot MK$ và $AM \bot KJ$.

Phương pháp giải

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải của GV Loigiaihay.com

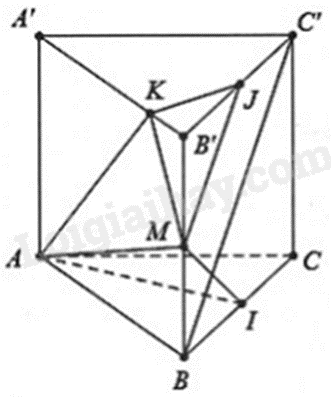
a) Vì tam giác ABC là tam giác đều và I là trung điểm của BC nên $AI \bot BC$.

Mặt khác, $AI \bot CC'\left( {do\;CC' \bot \left( {ABC} \right)} \right)$ và BC và CC’ cắt nhau tại C và nằm trong mặt phẳng (BCC’B’) nên $AI \bot \left( {BCC'B'} \right) \Rightarrow AI \bot BC'$

Dễ dàng chứng minh được tứ giác BCC’B’ là hình vuông nên $BC' \bot B'C$.

Vì M, I lần lượt là trung điểm của BB’, BC nên MI là đường trung bình của tam giác BB’C. Do đó, MI//B’C. Mà $BC' \bot B'C$ nên $MI \bot BC'$.

Lại có: $AI \bot BC'$ và MI và AI cắt nhau tại I và nằm trong mặt phẳng (AIM).

Do đó, $BC' \bot \left( {AIM} \right) \Rightarrow BC' \bot AM$.

b) Tam giác KMB’ vuông tại B’ nên $\tan \widehat {KMB'} = \frac{{KB'}}{{MB'}} = \frac{1}{2}$

Tam giác AMB vuông tại B nên $\tan \widehat {AMB} = \frac{{AB}}{{BM}} = 2$

Do đó, $\tan \widehat {KMB'} = \cot \widehat {AMB} \Rightarrow \widehat {KMB'} + \widehat {AMB} = {90^0}$

Suy ra, $\widehat {AMK} = {90^0} \Rightarrow AM \bot MK$

Mặt khác: $AM \bot BC'\left( {cmt} \right),MJ//BC'$ (do MJ là đường trung bình của tam giác B’C’B)$\Rightarrow AM \bot MJ$

Mà $AM \bot MK$. Do đó, $AM \bot \left( {MKJ} \right) \Rightarrow AM \bot KJ$.