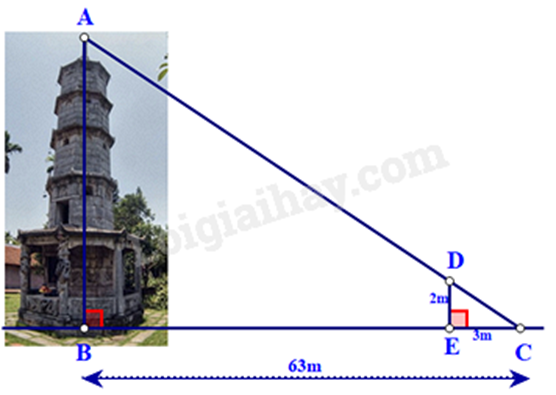
Bóng của một tháp trên mặt đất có độ dài BC = 63m. Cùng thời điểm đó, một cây cột DE cao 2 mét cắm vuông góc với mặt đất có bóng dài 3 mét. Tính chiều cao của tháp?
Áp dụng Định lí hai tam giác đồng dạng để chứng minh $\Delta ABC\backsim \Delta DEC$.
Từ đó suy ra tỉ số các cặp cạnh tương ứng để tính chiều cao của tháp.
Vì tháp và cây cột đều vuông góc với mặt đất nên ta có \(\widehat B = \widehat E = {90^0}\)
\( \Rightarrow \) AB // DE
$\Rightarrow \Delta ABC\backsim \Delta DEC$ (Định lí hai tam giác đồng dạng)
\(\begin{array}{l} \Rightarrow \frac{{AB}}{{DE}} = \frac{{BC}}{{CE}}\\\frac{{AB}}{2} = \frac{{63}}{3} = 21\\ \Rightarrow AB = 21.2 = 42\left( m \right)\end{array}\)
Vậy chiều cao của tháp là 42m.
Các bài tập cùng chuyên đề
Phân thức bằng với phân thức \(\frac{x}{{x - 1}}\) là:
Phân thức nghịch đảo của phân thức \(\frac{{x - y}}{{x + y}}\) là:
Giá trị của phân thức \(\frac{{{x^2} + 4x + 4}}{{{x^2} + 2x}}\) khi \(x = - 2\) là:
Kết quả phép tính \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 4}}{{x - 1}}\) là
Cho hình vẽ dưới đây, biết AB // DE. Giá trị của x là:
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AB, N là trung điểm của BC. Biết AB = 3cm, BC = 5cm. Khi đó MN bằng:
Một sân chơi có hình tam giác như hình dưới. Kích thước ba cạnh của sân lần lượt là 300m, 350m và 550m. Phía ngoài sân chơi có một con đường tạo thành một tam giác đồng dạng với sân chơi. Biết cạnh ngắn nhất của con đường là 450m. Tổng chiều dài của con đường đó là:
Cho $\Delta ABC\backsim \Delta MNP$ theo tỉ số đồng dạng 3. Gọi H, K lần lượt là trung điểm của AC, MP. Tỉ số \(\frac{{BH}}{{NK}}\) bằng
Thực hiện phép tính:
a) \(\frac{1}{{x + 1}} + \frac{2}{{1 - x}} + \frac{{5x - 1}}{{{x^2} - 1}}\)
b) \(\frac{{2x + 6}}{{{x^3} - 8}}:\frac{{{{\left( {x + 3} \right)}^3}}}{{2x - 4}}\)
Cho hai biểu thức \(P = \frac{{{x^2} - 2}}{{{x^2} + 2x}} + \frac{1}{{x + 2}}\), \(Q = \frac{{x + 1}}{x}\) (với \(x \ne 0\); \(x \ne - 2\); \(x \ne - 1\))
a) Tính giá trị của Q khi \(x = - 3\).
b) Rút gọn P.
c) Tìm \(x\) để \(P:Q = \frac{5}{2}\).
d) Tìm \(x\) nguyên để \(P\) có giá trị nguyên.
Cho tam giác ABC vuông tại A (AB > AC), đường cao AH. Từ B kẻ tia \(Bx \bot AB\), tia Bx cắt AH tại K.
a) Tứ giác ABKC là hình gì? Tại sao?
b) Chứng minh $\Delta ABK\backsim \Delta CHA$. Từ đó suy ra \(AB.AC = AK.CH\).
c) Chứng minh \(A{H^2} = HB.HC\).
d) Giả sử \(BH = 9cm,HC = 16cm\). Tính AB, AH.
Chứng minh rằng:
Nếu \(x = by + cz\); \(y = ax + cz\); \(z = ax + by\) và \(x + y + z \ne 0\) thì \(\frac{1}{{1 + a}} + \frac{1}{{1 + b}} + \frac{1}{{1 + c}} = 2\).
