Cho tứ diện ABCD. Gọi I là trung điểm của AB, J là điểm thuộc cạnh AD sao cho \(JA = 3JD\). Giao điểm của đường thẳng IJ và mặt phẳng (BDC) là:
-
A.
Giao điểm của IJ và BC.
-
B.
Giao điểm của IJ và DC.
-
C.
Giao điểm của IJ và AB.
-
D.
Giao điểm của IJ và DB.
Sử dụng kiến thức về cách tìm giao điểm của đường thẳng và mặt phẳng: Để tìm giao điểm của đường thẳng a và mặt phẳng \(\left( \alpha \right)\) ta làm như sau:
+ Tìm trong mặt phẳng \(\left( \alpha \right)\) đường thẳng b sao cho b cắt a tại A.
+ Khi đó, A là giao điểm của đường thẳng a và mặt phẳng \(\left( \alpha \right)\).
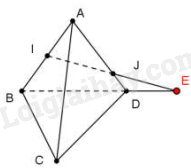
Trong mặt phẳng (ABD), gọi E là giao điểm của IJ và BD.
Ta có: \(\left\{ \begin{array}{l}E \in IJ\\E \in BD \subset \left( {CBD} \right)\end{array} \right.\) nên E là giao điểm của đường thẳng IJ và mặt phẳng (BDC).
Đáp án : D
Các bài tập cùng chuyên đề
Chọn đáp án đúng
Một cung của đường tròn bán kính R và có số đo \(\alpha \) rad thì có độ dài là:
Nghiệm của phương trình \(\cos x = 1\) là:
Hàm số \(y = \tan x\) đồng biến trên:
Chọn đáp án đúng:
Trong các dãy số sau, dãy số nào là dãy số giảm?
Trong các dãy số sau, dãy số nào là cấp số nhân?
Dãy số nào dưới đây được viết dưới dạng hệ thức truy hồi?
Biết \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a < 0\). Chọn đáp án đúng
Cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với công bội q, số hạng đầu \({u_1}\) thì có tổng là:
Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } {\left( {\frac{2}{3}} \right)^n}\) bằng:
Giá trị của \(\mathop {\lim }\limits_{x \to \frac{1}{3}} \left( {3x + 2} \right)\) là:
Chọn đáp án đúng.
Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD được gọi là hình gì?
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có bao nhiêu đường thẳng song song với đường thẳng đã cho?
Cho hình hộp ABCD. A’B’C’D’. Hình hộp này có bao nhiêu đường chéo?
Chọn đáp án đúng.
Chọn đáp án đúng:
Giá trị của biểu thức \(\cos \left( {\frac{\pi }{2} - \alpha } \right) - \sin \left( {\pi - \alpha } \right)\) bằng:
Cho tam giác ABC. Chọn đáp án đúng:
