Đề bài

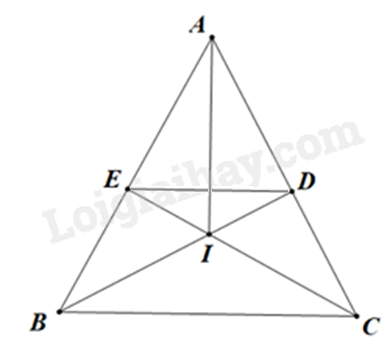
Cho $\Delta ABC$ cân tại $A$($\widehat A < 90^\circ$). Kẻ $BD \bot AC$tại $D$, kẻ $CE \bot AB$tại $E$.

a) Chứng minh: $\Delta ADE$cân.

b) Chứng minh: $DE//BC$.

c) Gọi $I$ là giao điểm của $BD$ và $CE$. Chứng minh: $IB = IC$.

d) Chứng minh: $AI \bot BC$.

Phương pháp giải

a) Chứng minh AD = AE nên tam giác ADE cân.

b) Chứng minh $\widehat {AED} = \widehat {ABC}$ (hai góc đồng vị) nên DE // BC.

c) Chứng minh tam giác BIC cân tại I nên IB = IC.

d) Chứng minh A và I cùng thuộc đường trung trực của BC nên $AI \bot BC$.

Lời giải của GV Loigiaihay.com

a) Xét $\Delta ADB$và $\Delta AEC$, có:

$\widehat A$: chung

$AB = AC$(vì $\Delta ABC$cân tại $A$)

$\widehat {ADB} = \widehat {AEC} = 90^\circ$(vì $BD \bot AC$tại $D$, $CE \bot AB$ tại $E$)

Suy ra $\Delta ADB = \Delta ACE$(cạnh huyền-góc nhọn).

Suy ra$AD = AE$(2 cạnh tương ứng).

Vậy $\Delta ADE$cân tại $A$.

b) Vì $\Delta ABC$cân tại $A$ (gt)

Ta có: $\widehat {ABC} = \frac{{{{180}^{\rm{o}}} - \widehat A}}{2}$  (1)

Lại có: $\Delta AED$ cân tại $A$ (câu a)

Nên $\widehat {AED} = \frac{{{{180}^{\rm{o}}} - \widehat A}}{2}$                 (2)

Từ (1) và (2) $\Rightarrow \widehat {AED} = \widehat {ABC}$

Mà $\widehat {AED}$ và $\widehat {ABC}$ ở vị trí đồng vị.

Vậy $DE//BC$.

c) Có tia $BD$ nằm giữa hai tia $BA,BC$.

Suy ra $\widehat {ABD} + \widehat {DBC} = \widehat {ABC}$

Suy ra $\widehat {DBC} = \widehat {ABC} - \widehat {ABD}$

Tương tự, có:

$\widehat {ECB} = \widehat {ACB} - \widehat {ACE}$

Mà $\widehat {ABC} = \widehat {ACB}$ (do $\Delta ABC$cân tại $A$)

$\widehat {ADB} = \widehat {ACE}$ (vì $\Delta ADB = \Delta AEC$)

Suy ra $\widehat {DBC} = \widehat {ECB}$

Vậy $\Delta IBC$ cân tại $I$.

Suy ra $IB = IC$

d) Có: $AB = AC$ (vì $\Delta ABC$cân tại $A$)

Do đó$A$ thuộc đường trung trực của $BC$

Lại có: $IB = IC$(câu c)

Suy ra $I$ thuộc đường trung trực của $BC$

Suy ra $AI$ là đường trung trực của $BC$

Suy ra $AI \bot BC$.