Đề bài

Cho hình vẽ sau có \(\widehat {CBA} = 50^\circ \). Số đo \(\widehat D\) bằng

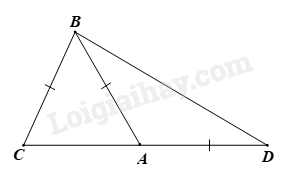
• A. \(40^\circ \).
• B. \(45^\circ \).
• C. \(32,5^\circ \).   
• D. \(35^\circ \).

Phương pháp giải

- Dựa vào tính chất của tam giác cân

- Tính chất tổng 3 góc của tam giác bằng 180⁰.

- Tính chất hai góc kề bù.

Lời giải của GV Loigiaihay.com

Xét tam giác ABC có AB = BC nên tam giác ABC cân tại B.

\( \Rightarrow \widehat {BAC} = \widehat {BCA}\)

Mà \(\widehat {CBA} = 50^\circ \) nên \(\widehat {BAC} = \widehat {BCA} = \frac{{{{180}^0} - {{50}^0}}}{2} = {65^0}\).

\(\widehat {BAC} + \widehat {BAD} = {180^0} \Rightarrow \widehat {BAD} = {180^0} - {65^0} = {115^0}\).

Xét tam giác ABD có AB = AD nên tam giác ABD cân tại A \( \Rightarrow \widehat {ABD} = \widehat {ADB} = \frac{{{{180}^0} - {{115}^0}}}{2} = 32,{5^0}\).

Đáp án : C