Kết quả tìm hiểu về sở thích chơi game của một số học sinh trong một trường
THCS được ghi bởi bảng thống kê sau. Hãy cho biết nhiều học sinh lựa chọn loại nào nhất?
-
A.
Thích.
-
B.
Rất thích.
-
C.
Không thích.
-
D.
Thích ít.
Quan sát bảng thống kê, lập bảng số liệu biểu thị sở thích chơi game của các học sinh đó theo số lượng để biết học sinh lựa chọn loại nào nhiều nhất.
Ta có bảng số liệu sở thích chơi game của các học sinh theo số lượng như sau:
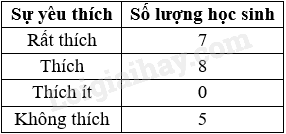
Quan sát bảng số liệu trên, ta thấy học sinh lựa chọn “Thích” có số lượng nhiều nhất.
Đáp án : A
Các bài tập cùng chuyên đề
Khẳng định nào sau đây sai:
Số đối của \(\frac{5}{6}\) là:
Căn bậc hai số học của 196 là:
Số nào là số vô tỉ trong các số sau:
Cho \(\widehat {{\rm{xOy}}} = {70^0}\)và tia Ot là tia phân giác của \(\widehat {{\rm{xOy}}}\). Số đo \(\widehat {{\rm{xOt}}}\) bằng:
Cho hình vẽ bên, biết \({\widehat {\rm{O}}_1} = {60^0}\). Số đo \({\widehat {\rm{O}}_3}\) là:
Đường trung trực của một đoạn thẳng là
Cho hai tam giác \(\Delta ABC\) và \(\Delta MNP\) có \(\widehat B = \widehat P\), \(BC = PN\). Cần thêm điều kiện nào để \(\Delta ABC = \Delta MPN\) theo trường hợp góc – cạnh – góc
Trong các dữ liệu sau, dữ liệu nào không phải là dữ liệu định lượng?
Cho hình vẽ sau có \(\widehat B = {48^O},\widehat {AED} = {65^O}\). Số đo \(\widehat {BAD}\) bằng
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) xếp loại học lực giữa kì I của học sinh lớp 7A. Hỏi học sinh đạt loại gì là nhiều nhất?
Thực hiện phép tính:
a) \({\left( {\frac{2}{3} - 1} \right)^2} - \frac{3}{5}:\frac{9}{{10}} + {1^{2022}}\).
b) \(\frac{8}{7} \cdot \left| {\frac{{ - 3}}{5}} \right| + \frac{8}{7} \cdot \sqrt {\frac{4}{{25}}} - \frac{{\sqrt 9 }}{4}\).
Tìm x, biết:
a) \(x + 0,75 = \frac{2}{3}\).
b) \(\left| {\frac{1}{2} - x} \right| = \frac{4}{5}\).
Diện tích nước Việt Nam là 331 698 km2. Hãy làm tròn diện tích này đến hàng nghìn.
Cho \(\widehat {xOy}\) nhọn. Trên \(Ox\) lấy điểm \(A\) và trên \(Oy\) lấy điểm \(B\) sao cho \(OA = OB\). Vẽ ra phía ngoài \(\widehat {xOy}\) hai đoạn \(AM = BN\) sao cho \(AM \bot Ox\) và \(BN \bot Oy\). Chứng minh:
a. \(\Delta OMA = \Delta ONB\).
b. \(\widehat {AON\,}\)= \(\widehat {BOM}\) và \(\widehat {OMB}\)=\(\widehat {ONA}\).
Cho hình vẽ bên, biết: \(m \bot a;m \bot b;\widehat {CDb} = {110^0}\).
a) Chứng minh: a // b
b) Tính số đo: \({\widehat {\rm{D}}_1}\) và \(\widehat {{\rm{ ACD}}}\)
(Học sinh vẽ lại hình vào bài làm)
