Đề bài

1. Một giá đèn cầy có dạng hình chóp tứ giác đều như hình bên có độ dài cạnh đáy là 14cm; các cạnh bên có độ dài bằng $17\sqrt 2$cm

Tính thể tích của giá đèn cầy có dạng hình chóp tứ giác đều với kích thước như trên. (Làm tròn đến hàng đơn vị).

2. Cho hình thang cân $ABCD$ $(AB\parallel CD,AB < CD)$, các đường cao $AH$, $BK$.

a) Tứ giác $ABKH$ là hình gì? Vì sao?

b) Chứng minh $DH = CK$.

c) Tứ giác $ABCE$ là hình gì?

Phương pháp giải

1. Dựa vào định lí Pythagore và công thức tính thể tích giá đèn cầy để tính.

2.

a) Tứ giác $ABKH$ là hình chữ nhật.

b) $\Delta ADH = \Delta BKC$ (ch - gn).

Nên suy ra $DH = KC$.

c) Dễ thấy $HE + EK = EK + KC$ $\Rightarrow$ $AB = EC$. Do đó, $ABCE$ là hình bình hành.

Lời giải của GV Loigiaihay.com

1. 

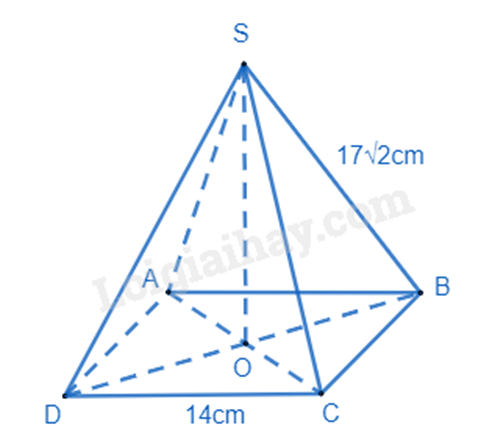
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông, SO là đường cao của hình chóp S.ABCD.

Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore, ta có:

$A{C^2} = A{B^2} + B{C^2} = {14^2} + {14^2} = 128$ suy ra $AC = \sqrt {128} = 14\sqrt 2 (cm)$

Do đó $AO = \frac{{14\sqrt 2 }}{2} = 7\sqrt 2 (cm)$

Xét tam giác SAO vuông tại O, áp dụng định lí Pythagore, ta có:

$S{O^2} = S{A^2} - A{O^2} = {\left( {17\sqrt 2 } \right)^2} - {\left( {7\sqrt 2 } \right)^2} = 480$

suy ra $SO = 4\sqrt {30}(cm)$

Thể tích giá đèn cầy S.ABCD là:

$V = \frac{1}{3}{.4\sqrt {30}.14^2} \approx 1431\left( {c{m^3}} \right)$

Vậy thể tích giá đèn cầy là 1431cm³.

2. 

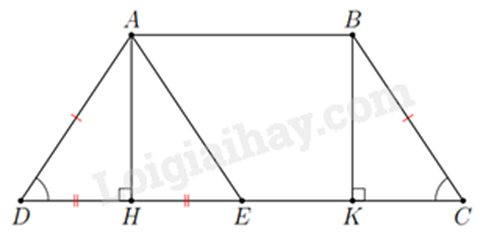
a) Ta có: AB // CD (ABCD là hình thang cân), AH $\bot$ CD => AH $\bot$ AB => $\widehat {BAH} = {90^0}$.

Xét tứ giác ABKH có: $\widehat {BAH} = {90^0};\widehat H = {90^0};\widehat K = {90^0}$ suy ra ABKH là hình chữ nhật.

b) ABKH là hình chữ nhật => AH = BK.

ABCD là hình thang cân nên AD = BC.

Xét tam giác AHD và BKC có:

$\left\{ \begin{array}{l}AD = BC\\AH = BK(cmt)\\\widehat H = \widehat K = {90^0}\end{array} \right. \Rightarrow \Delta AHD = \Delta BKC(ch - cgv)$

=> DH = CK. (đpcm)

c) Ta có: AB = HK (ABKH là hình chữ nhật)

Ta có E đối xứng với D qua H => DH = HE => HK = HE + EK = DH + EK = KC + EK = EC.

=> AB = EC.

Mà AB // CE, do đó ABCE là hình bình hành.