Cho hình vẽ:

Chọn đáp án đúng.
-
A.
\(y = 10\)
-
B.
\(x = 4,8\)
-
C.
A, B đều đúng
-
D.
A, B đều sai
Tam giác ADO và tam giác ECO có: \(\widehat {DAO} = \widehat {CEO} = {90^0},\widehat {AOD} = \widehat {COE}\) (hai góc đối đỉnh)
Do đó, \(\Delta ADO \backsim \Delta ECO \Rightarrow \frac{{AD}}{{EC}} = \frac{{DO}}{{CO}} \Rightarrow \frac{4}{x} = \frac{5}{6} \Rightarrow x = 4,8\)
Áp dụng định lý Pytago vào tam giác ADO vuông tại A ta có:
\(A{D^2} + A{O^2} = O{D^2}\) \( \Rightarrow A{O^2} = D{O^2} - A{D^2} = 9 \Rightarrow AO = 3\)
Tam giác CEO và tam giác CAB có: \(\widehat {CEO} = \widehat {CAB} = {90^0},\widehat {C}\;chung\)
Do đó, \(\Delta CEO \backsim \Delta CAB \Rightarrow \frac{{CO}}{{CB}} = \frac{{CE}}{{CA}} \Rightarrow \frac{{CO}}{{EC + EB}} = \frac{{CE}}{{CO + AO}} \Rightarrow \frac{6}{{4,8 + y}} = \frac{{4,8}}{{6 + 3}} \Rightarrow y = 6,45\)
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\widehat B = \widehat F\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
Bài 2 :
Cho hình vẽ:

Chọn đáp án đúng
-
A.
\(\Delta IPQ \backsim \Delta IMN\)
-
B.
\(\Delta IPQ = \Delta IMN\)
-
C.
\(\Delta IPQ \backsim \Delta INM\)
-
D.
\(\Delta IPQ \backsim \Delta MNI\)
Bài 3 :
Cho tam giác ABC vuông tại A và DEF vuông tại D. Để \(\Delta ABC \backsim \Delta DEF\) thì ta cần thêm điều kiện:
-
A.
\(\widehat B = \widehat E\)
-
B.
\(\widehat B = \widehat F\)
-
C.
\(\widehat B = \frac{1}{2}\widehat E\)
-
D.
\(\widehat B = \frac{1}{2}\widehat F\)
Bài 4 :
Cho các mệnh đề sau. Chọn câu đúng.
(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
(II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
-
A.
(I) đúng, (II) sai
-
B.
(I) sai, (II) đúng
-
C.
(I) và (II) đều sai
-
D.
(I) và (II) đều đúng
Bài 5 :
Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
-
A.
\(\Delta ACH \backsim \Delta BCA\)
-
B.
\(\Delta ACH \backsim \Delta CBA\)
-
C.
\(\Delta ACH \backsim \Delta BAC\)
-
D.
\(\Delta ACH \backsim \Delta CBA\)
Bài 6 :
Cho hình vẽ:
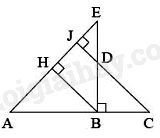
Chọn đáp án đúng.
-
A.
\(\frac{{BC}}{{BE}} = 2\frac{{BD}}{{BA}}\)
-
B.
\(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)
-
C.
\(2\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)
-
D.
A, B, C đều sai
Bài 7 :
Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho \(AM = 2m,AM \bot AB\) và đo được góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A’M’B’ vuông tại A’ có \(A'M' = 1cm,\;\widehat {A'M'B'} = \widehat {AMB}\) và đo được \(A'B' = 5cm\) (hình vẽ dưới). Khoảng cách từ A đến B bằng:

-
A.
4m
-
B.
6m
-
C.
8m
-
D.
10m
Bài 8 :
Một ngọn tháp cho như hình vẽ dưới đây, biết rằng \(MB = 20m,MF = 2m,FE = 1,65m.\)

Chiều cao AB của ngọn tháp bằng:
-
A.
17,5m
-
B.
14,5m
-
C.
16,5m
-
D.
15,5m
Bài 9 :
Cho hình vẽ:
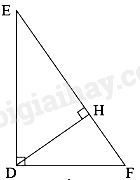
Khẳng định nào sau đây là đúng?
-
A.
\(D{H^2} = HE + 2HF\)
-
B.
\(D{H^2} = HE.HF\)
-
C.
\(D{H^2} = HE + HF\)
-
D.
\(D{H^2} = HE - HF\)
Bài 10 :
Cho tam giác ABC vuông tại A có \(\widehat B = {30^0}\), tam giác MNP vuông tại M có \(\widehat N = {60^{0.}}\)
Chọn đáp án đúng.
-
A.
\(AB.PN = MP.BC\)
-
B.
\(AB.MP = PN.BC\)
-
C.
\(AB.MP = 2PN.BC\)
-
D.
\(AB.PN = 2MP.BC\)
Bài 11 :
Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
-
A.
\(2AC = CH.BC\)
-
B.
\(A{C^2} = \frac{1}{2}CH.BC\)
-
C.
\(A{C^2} = CH.BC\)
-
D.
\(A{C^2} = 2CH.BC\)
Bài 12 :
Cho tam giác \(ABC\) cân tại \(A\) , đường cao \(CE\) . Tính \(AB\) , biết \(BC = 24\) cm và \(BE = 9\) cm.
-
A.
16cm
-
B.
32cm
-
C.
24cm
-
D.
18cm
Bài 13 :
Cho hình vẽ:
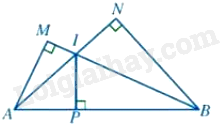
Chọn đáp án đúng
-
A.
\(AI.AN + BI.BM = 2A{B^2}\)
-
B.
\(AI.AN + BI.BM = A{B^2}\)
-
C.
\(AI.AN + 2BI.BM = A{B^2}\)
-
D.
\(2AI.AN + BI.BM = A{B^2}\)
Bài 14 :
Cho hình vẽ:

Chọn đáp án đúng
-
A.
\(AC.AK = \frac{1}{2}AB.AI\)
-
B.
\(AC.AK = 2AB.AI\)
-
C.
\(AC.AK = 3AB.AI\)
-
D.
\(AC.AK = AB.AI\)
Bài 15 :
Cho tam giác ABC cân tại A, \(AC = 20cm,BC = 24cm.\) Các đường cao AD và CE cắt nhau tại H. Khi đó,
-
A.
\(HD = 12cm\)
-
B.
\(HD = 6cm\)
-
C.
\(HD = 9cm\)
-
D.
\(HD = 10cm\)
Bài 16 :
Cho tam giác ABC vuông tại A, đường cao AH chia đoạn BC thành hai đoạn thẳng \(HB = 7cm,HC = 18cm.\) Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác thành 2 phần có diện tích bằng nhau. Khi đó,
-
A.
\(CE = 15cm\)
-
B.
\(CE = 16cm\)
-
C.
\(CE = 12cm\)
-
D.
\(CE = 10cm\)
Bài 17 :
Cho hình bình hành ABCD \(\left( {AC > AB} \right)\) . Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD và H là hình chiếu của B trên AC.
Chọn đáp án đúng.
-
A.
\(AB.AE + AD.AK = 2A{C^2}\)
-
B.
\(2AB.AE + AD.AK = A{C^2}\)
-
C.
\(AB.AE + 2AD.AK = A{C^2}\)
-
D.
\(AB.AE + AD.AK = A{C^2}\)
Bài 18 :
Cho tam giác ABC vuông tại A. Lấy một điểm M bất kì trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E. Khi đó:
-
A.
\(BM.BD + CM.CA = \frac{1}{2}B{C^2}\)
-
B.
\(BM.BD + 2CM.CA = B{C^2}\)
-
C.
\(BM.BD + CM.CA = B{C^2}\)
-
D.
\(BM.BD + CM.CA = 2B{C^2}\)
Bài 19 :
Cho tam giác ABC cân tại A, đường cao CE. Biết rằng \(BE = 3cm,BC = 8cm.\)
Độ dài đoạn thẳng AB là:
-
A.
\(\frac{{34}}{3}cm\)
-
B.
32cm
-
C.
\(\frac{{32}}{3}cm\)
-
D.
35cm
Bài 20 :
Cho hình vẽ. Khẳng định nào sao đây đúng
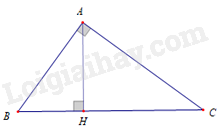
-
A.
\(\Delta ABC\,\backsim \Delta ABH\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta HAB\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta AHB\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta HBA\) .
Bài 21 :
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\). Hệ thức nào sau đây đúng?
-
A.
\(AB = BC.BH\).
-
B.
\(A{C^2} = CH.BH\).
-
C.
\(A{H^2} = BH.CH\).
-
D.
\(AH = CH.BH\).
Bài 23 :
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\) biết \(BH = 4\,{\rm{cm}}\), \(CH = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(AH\) là
-
A.
\(4,8\,{\rm{cm}}\).
-
B.
\(5\,{\rm{cm}}\).
-
C.
\(6\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
Bài 24 :
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 30\,{\rm{cm}}\), \(AC = 40\,{\rm{cm}}\). Kẻ đường cao \(AH\)\(\left( {H \in BC} \right)\). Độ dài đường cao \(AH\) là
-
A.
\(18\,{\rm{cm}}\).
-
B.
\(24\,{\rm{cm}}\).
-
C.
\(32\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
Bài 25 :
\(\Delta ABC\) cân tại \(A\), hai đường cao \(AH\) và \(BK\), cho \(BC = 6\,{\rm{cm}}\), \(AB = 5\,{\rm{cm}}\). Độ dài đoạn thẳng \(BK\) là
-
A.
\(4,5\,{\rm{cm}}\).
-
B.
\(4,8\,{\rm{cm}}\).
-
C.
\(3\,{\rm{cm}}\).
-
D.
\(4\,{\rm{cm}}\).
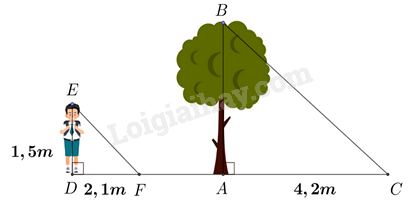
Bài 26 :
Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.
-
A.
\(AB = 3m\).
-
B.
\(AB = 0,75m\).
-
C.
\(AB = 2,4m\).
-
D.
\(AB = 2,25m\).
Bài 27 :
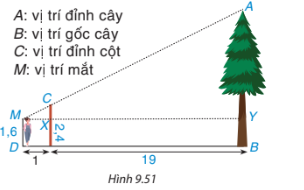
Một người đo chiều cao của một cái cây bằng cách cắm một chiếc cọc xuống đất, cọc cao 2,4m và cách vị trí gốc cây 19m. Người đo đứng cách xa chiếc cọc 1m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m(H9.51)
A: Vị trí đỉnh cây
B: Vị trí gốc cây
C: Vị trí đỉnh cột.
D: Vị trí mắt
Bài 28 :
Nam và Việt muốn đo chiều cao của cột cờ ở sân trường mà hai bạn không trèo lên được. Vào buổi chiều, Nam đo thấy bóng của cột cờ dài 6m và bóng của Việt dài 70cm. Nam hỏi Việt cao bao nhiêu, Việt trả lời là cao 1,4m. Nam liền reo lên: "Tớ biết cột cờ cao bao nhiêu rồi đấy" Vậy cột cờ cao bao nhiêu và làm sao bạn Nam biết được.
Ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc vuông của tam giác ABC vuông tại đỉnh A, bạn Việt và bóng của mình cũng được xem là hai canh góc vuông của tam giác A'B'C' vuông tại đỉnh A'. Vì các tia sáng mặt trời tạo với hai cái bóng các góc bằng nhau nên \(\widehat B = \widehat {B'}\)
a) Hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không?
b) Bạn Nam đã tính chiều cao chiếc cột, tức là độ dài đoạn thẳng AC như thế nào và kết quả là bao nhiêu?

Bài 29 :
Cho góc nhọn xOy, các điểm A, N nằm trên tia Ox, các điểm B, M nằm trên tia Oy sao cho AM, BN lần lượt vuông góc với Oy, Ox. Chứng minh tam giác OAM đồng dạng với tam giác OBN.
Bài 30 :
Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho AM = 2 m, AM vuông góc với AB và đo được số đo góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A'M'B' vuông tại A' có AM' = 1cm, \(\widehat {A'M'B'} = \widehat {AMB}\) và đo được A'B' = 5 cm (H.9.56). Hỏi khoảng cách từ A đến B là bao nhiêu mét?



















Danh sách bình luận