Cho hai hình bình hành \(ABCD\) và \(ABEF\) lần lượt có tâm \({O_1},{O_2}\) và không cùng nằm trong một mặt phẳng. Mệnh đề nào sau đây sai?
-
A.
\({O_1}{O_2}\parallel \left( {CDE} \right)\).
-
B.
\({O_1}{O_2}\parallel \left( {BCE} \right)\).
-
C.
\({O_1}{O_2}\parallel \left( {BDE} \right)\).
-
D.
\({O_1}{O_2}\parallel \left( {ADF} \right)\).
Sử dụng định lí: Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).
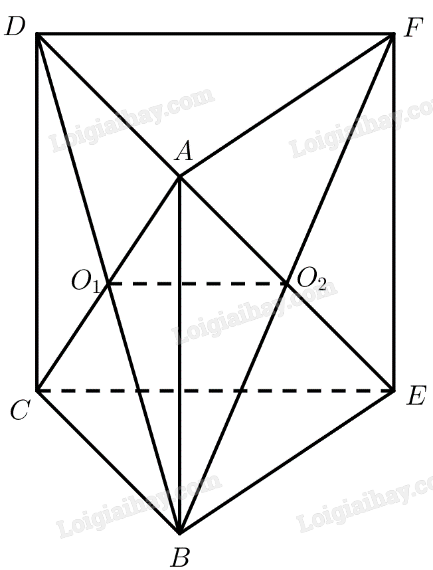
Vì \({O_1}\) là trung điểm của \(AC\), \({O_2}\) là trung điểm của \(AE\)
\( \Rightarrow {O_1}{O_2}\) là đường trung bình của tam giác \(AC{\rm{E}}\)\( \Rightarrow {O_1}{O_2}\parallel CE\)
Ta có:
\(\left. \begin{array}{l}{O_1}{O_2}\parallel CE\\C{\rm{E}} \subset \left( {C{\rm{D}}E} \right)\end{array} \right\} \Rightarrow {O_1}{O_2}\parallel \left( {C{\rm{D}}E} \right)\)
Ta có:
\(\left. \begin{array}{l}{O_1}{O_2}\parallel CE\\C{\rm{E}} \subset \left( {BCE} \right)\end{array} \right\} \Rightarrow {O_1}{O_2}\parallel \left( {BCE} \right)\)
Tương tự, \({O_1}\) là trung điểm của \(B{\rm{D}}\), \({O_2}\) là trung điểm của \(BF\)
\( \Rightarrow {O_1}{O_2}\) là đường trung bình của tam giác \(B{\rm{D}}F\)\( \Rightarrow {O_1}{O_2}\parallel DF\)
Khi đó,
\(\left. \begin{array}{l}{O_1}{O_2}\parallel DF\\DF \subset \left( {A{\rm{D}}F} \right)\end{array} \right\} \Rightarrow {O_1}{O_2}\parallel \left( {A{\rm{D}}F} \right)\)
Đáp án : C

Các bài tập cùng chuyên đề

















