Đề bài

Cho hình chóp S.ABC và G, K lần lượt là trọng tâm tam giác SAB, SBC. Khẳng định nào sau đây là đúng?

• A. GK // AC
• B. GK // AB
• C. GK // BC
• D. GK // SB

Phương pháp giải

Sử dụng tính chất trọng tâm của tam giác và định lý Ta lét để chứng minh.

Định lý Ta lét: Nếu một đường thẳng cắt 2 cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ững tỉ lệ thì nó song song với cạnh còn lại của tam giác.

Lời giải của GV Loigiaihay.com

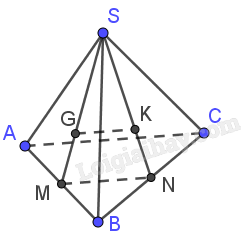
Gọi M, N lần lượt là trung điểm của AB, BC.

Vì G, K lần lượt là trọng tâm tam giác SAB, SBC. Khi đó:

\(\frac{{SG}}{{SM}} = \frac{2}{3};\frac{{SK}}{{SN}} = \frac{2}{3} \Rightarrow \frac{{SG}}{{SM}} = \frac{{SK}}{{SN}}\)

Theo định lý Ta lét suy ra, GK // MN mà MN // AC.

Do đó GK // AC.

Đáp án : A