Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi I, J lần lượt là trung điểm SA, SC. Đường thẳng IJ song song với đường thẳng nào trong các đường thẳng sau?

• A. BD
• B. BC
• C. AC
• D. SO

Phương pháp giải

Vẽ hình và sử dụng tính chất đường trung bình của tam giác để chứng minh.

Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

Lời giải của GV Loigiaihay.com

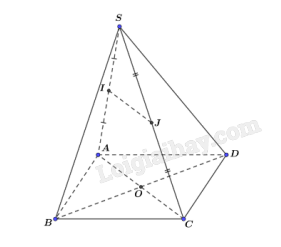
Vì I, J lần lượt là trung điểm SA, SC.

Suy ra, IJ là đường trung bình tam giác SAC nên IJ // AC.

Đáp án : C