Đề bài

Cân nặng của lợn con giống A và giống B được thống kê như bảng sau:

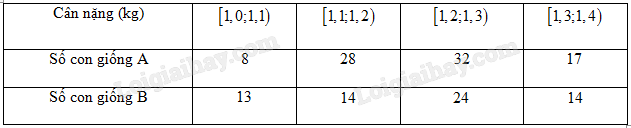
Hãy ước lượng trung vị và tứ phân vị thứ nhất của cân nặng lợn con mới sinh giống \(A\) và của cân nặng lợn con mới sinh giống \(B\).

• A. \({M_A} = 1,22;{Q_{1A}} = 1,15;{M_B} = 1,223;{Q_{1B}} = 1,12\)
• B. \({M_A} = 1,22;{Q_{1A}} = 1,45;{M_B} = 1,223;{Q_{1B}} = 1,12\)
• C. \({M_A} = 1,22;{Q_{1A}} = 1,15;{M_B} = 1,43;{Q_{1B}} = 1,12\)
• D. \({M_A} = 1,02;{Q_{1A}} = 1,15;{M_B} = 1,223;{Q_{1B}} = 1,12\)

Phương pháp giải

Công thức xác định trung vị của mẫu số liệu ghép nhóm

Để tìm trung vị của một mẫu số liệu, ta thực hiện như sau:

Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm.

Nếu số giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.

Công thức xác định tứ phân vị của mẫu số liệu ghép nhóm

Tứ phận vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu là \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.

Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta thực hiện như sau:

Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất;

\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất;

\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).

Khi đó  \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).

Tương tự, để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta thực hiện như sau:

Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba;

\({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba;

\(C = {n_1} + {n_2} + ... + {n_{j - 1}}\).

Khi đó \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\).

Lời giải của GV Loigiaihay.com

Gọi \({x_1};{x_2};{x_3}; \ldots ;{x_{85}}\) lần lượt là số lợn con giống \({\rm{A}}\) theo thứ tự không gian

Do \({x_1}, \ldots ,{x_8} \in \left[ {1,0;1,1} \right);{x_9}, \ldots ,{x_{36}} \in \left[ {1,1;1,2} \right);{x_{37}}, \ldots ,{x_{68}} \in \left[ {1,2;1,3} \right)\) \({x_{69}}, \ldots ,{x_{85}} \in \left[ {1,3;1,4} \right)\)
Trung vị của mẫu số liệu lợn con giống A thuộc nhóm \(\left[ {1,2;1,3} \right)\)

\({M_A} = 1,2 + \frac{{\frac{{85}}{2} - 36}}{{32}} \cdot \left( {1,3 - 1,2} \right) = 1,22\)

Gọi \({y_1};{y_2};{y_3}; \ldots ;{y_{65}}\) lần lượt là số lợn con giống \({\rm{B}}\) theo thứ tự không gian.
Do \({y_1}, \ldots ,{y_{13}} \in \left[ {1,0;1,1} \right);{y_{14}}, \ldots ,{y_{27}} \in \left[ {1,1;1,2} \right);{y_{28}}, \ldots ,{y_{51}} \in \left[ {1,2;1,3} \right)\); \({y_{52}}, \ldots ,{y_{65}} \in \left[ {1,3;1,4} \right)\)

Trung vị của mẫu số liệu lợn con giống B thuộc nhóm \(\left[ {1,2;1,3} \right)\).

\({M_B} = 1,2 + \frac{{\frac{{65}}{2} - 27}}{{24}} \cdot \left( {1,3 - 1,2} \right) = 1,223\).

Vậy cân nặng trung bình của lợn con giống A nhỏ hơn giống B.
b) Tứ phân vị thứ nhất của dãy số liệu giống \({\rm{A}}\) là \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\) thuộc nhóm \(\left[ {1,1;1,2} \right)\) nên tứ phân vị thứ nhất của mẫu số liệu là \({Q_{1A}} = 1,1 + \frac{{\frac{{85}}{4} - 8}}{{28}}\left( {1,2 - 1,1} \right) = 1,15\).

Tứ phân vị thứ nhất của dãy số liệu giống \({\rm{B}}\) là \(\frac{1}{2}\left( {{y_{16}} + {y_{17}}} \right)\) thuộc nhóm \(\left[ {1,1;1,2} \right)\) nên tứ phân vị thứ nhất của mẫu số liệu là \({Q_{1B}} = 1,1 + \frac{{\frac{{65}}{4} - 13}}{{14}}\left( {1,2 - 1,1} \right) = 1,12\).

Đáp án : A