Đề bài

Bảng 13 cho ta bảng tần số ghép nhóm số liệu thống kê cân nặng của 40 học sinh lớp \(11{\rm{\;A}}\) trong một trường trung học phổ thông (đơn vị: kilôgam).

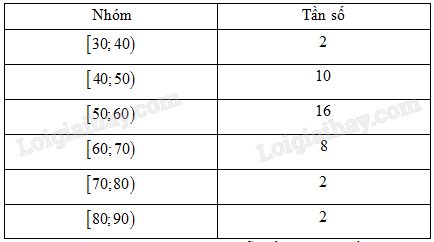
Hãy ước lượng các tứ phân vị của mẫu số liệu ghép số trên.

• A. \({Q_1} = 49\left( {{\rm{\;kg}}} \right);{Q_2} = 50\left( {{\rm{\;kg}}} \right);{Q_3} = 52,5\left( {{\rm{\;kg}}} \right)\)
• B. \({Q_1} = 48\left( {{\rm{\;kg}}} \right);{Q_2} = 55\left( {{\rm{\;kg}}} \right);{Q_3} = 62,5\left( {{\rm{\;kg}}} \right)\)
• C. \({Q_1} = 47\left( {{\rm{\;kg}}} \right);{Q_2} = 54\left( {{\rm{\;kg}}} \right);{Q_3} = 63,5\left( {{\rm{\;kg}}} \right)\)
• D. \({Q_1} = 46\left( {{\rm{\;kg}}} \right);{Q_2} = 53\left( {{\rm{\;kg}}} \right);{Q_3} = 64,5\left( {{\rm{\;kg}}} \right)\)

Phương pháp giải

Công thức xác định tứ phân vị của mẫu số liệu ghép nhóm

Tứ phận vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu là \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.

Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta thực hiện như sau:

Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất;

\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất; \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).

Khi đó  \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).

Tương tự, để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta thực hiện như sau:

Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba;

\({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba;

\(C = {n_1} + {n_2} + ... + {n_{j - 1}}\).

Khi đó \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\).

Lời giải của GV Loigiaihay.com

Số phần tử của mẫu là \(n = 40\).

Áp dụng công thức, ta có tứ phân vị thứ nhất là: \({Q_1} = 40 + \left( {\frac{{10 - 2}}{{10}}} \right) \cdot 10 = 48\left( {{\rm{\;kg}}} \right).\)

Áp dụng công thức, ta có tứ phân vị thứ hai là:\({Q_2} = {M_e} = 50 + \left( {\frac{{20 - 12}}{{16}}} \right) \cdot 10 = 55\left( {{\rm{\;kg}}} \right).\)

Áp dụng công thức, ta có tứ phân vị thứ ba là: \({Q_3} = 60 + \left( {\frac{{30 - 28}}{8}} \right).10 = 62,5\left( {{\rm{\;kg}}} \right).\)

Vậy tứ phân vị của mẫu số liệu trên là: \({Q_1} = 48\left( {{\rm{\;kg}}} \right);{Q_2} = 55\left( {{\rm{\;kg}}} \right);{Q_3} = 62,5\left( {{\rm{\;kg}}} \right)\).

Đáp án : B