Một đu quay ở công viên có bán kính bằng 10 m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay được góc \(270^o\) ?
-
A.
\(\frac{2}{3}\) phút
-
B.
\(\frac{1}{3}\) phút
-
C.
\(\frac{1}{4}\) phút
-
D.
\(\frac{1}{2}\) phút
Tính thời gian quay hết 1 vòng.
Đổi \(270^o\) ra số phần vòng quay được.
Tính thời gian quay được số phần vòng đó (dựa vào thời gian quay đủ 1 vòng).
Đổi \({270^o} = {270^o} .\frac{\pi }{{{{180}^o}}} = \frac{{3\pi }}{2} = \frac{3}{4}.2\pi \).
Suy ra đu quay quay được \(270^o\) khi nó quay được \(\frac{3}{4}\) vòng.
Đu quay quay được 1 vòng trong \(\frac{1}{3}\) phút.
Do đó đu quay quay được \(\frac{3}{4}\) vòng trong \(\frac{1}{3}.\frac{3}{4} = \frac{1}{4}\) phút.
Đáp án : C
Đổi đơn vị đo góc từ độ dang radian
\({\alpha ^o} = {\alpha ^o}.\frac{\pi }{{{{180}^o}}} = \frac{{\alpha \pi }}{{180}}rad\).

Các bài tập cùng chuyên đề
Bài 1 :
Đổi số đo của góc \({70^0}\) sang đơn vị radian.
-
A.
\(\dfrac{{70}}{\pi }.\)
-
B.
\(\dfrac{7}{{18}}.\)
-
C.
\(\dfrac{{7\pi }}{{18}}.\)
-
D.
\(\dfrac{7}{{18\pi }}.\)
Bài 2 :
Đổi số đo của góc \( - \dfrac{{3\pi }}{{16}}{\rm{ rad}}\) sang đơn vị độ, phút, giây.
-
A.
\({33^0}45'.\)
-
B.
\( - {29^0}30'.\)
-
C.
\( - {33^0}45'.\)
-
D.
\( - {32^0}55.\)
Bài 3 :
Góc có số đo ${108^{\rm{o}}}$ đổi ra radian là
-
A.
$\dfrac{{3\pi }}{5}.$
-
B.
$\dfrac{\pi }{{10}}.$
-
C.
$\dfrac{{3\pi }}{2}.$
-
D.
$\dfrac{\pi }{4}.$
Bài 4 :
Góc có số đo \({120^{\rm{o}}}\) đổi sang rađian là góc
-
A.
\(\dfrac{\pi }{{10}}.\)
-
B.
\(\dfrac{{3\pi }}{2}.\)
-
C.
\(\dfrac{\pi }{4}.\)
-
D.
\(\dfrac{{2\pi }}{3}.\)
Bài 5 :
Góc có số đo \({120^o}\) đổi sang radian là:
-
A.
\(\dfrac{{3\pi }}{2}\).
-
B.
\(\dfrac{{2\pi }}{3}\).
-
C.
\(\dfrac{\pi }{4}\).
-
D.
\(\dfrac{\pi }{{10}}\).
Bài 6 :
Góc \(\dfrac{{5\pi }}{6}\) có số đo theo độ là
-
A.
\({112^o}50'\)
-
B.
\( - {150^o}\)
-
C.
\({120^o}\)
-
D.
\({150^o}\)
Bài 7 :
Cung có số đo 2250 được đổi sang số đo rad là :-
A.
\(225\pi \)
-
B.
\(\dfrac{{3\pi }}{4}\)
-
C.
\(\dfrac{{5\pi }}{4}\).
-
D.
\(\dfrac{{4\pi }}{3}\)
Bài 8 :
Góc \(\dfrac{{7\pi }}{6}\) có số đo bằng độ là:-
A.
\({30^o}\)
-
B.
\({105^o}\)
-
C.
\({150^o}\)
-
D.
\({210^o}\)
Bài 9 :
Công thức nào sau đây là đúng về mối quan hệ giữa độ và rad?
-
A.
\({1^o} = \frac{\pi }{{360}}\) rad
-
B.
\({1^o} = \frac{\pi }{{180}}\) rad
-
C.
1 rad\( = - {\left( {\frac{{90}}{\pi }} \right)^o}\)
-
D.
1 rad\( = {\left( {\frac{{90}}{\pi }} \right)^o}\)
Bài 10 :
a) Đổi từ độ sang rađian các số đo sau: \({360^ \circ }, - {450^ \circ }\)
b) Đổi từ rađian sang độ các số đo sau: \(3\pi , - \frac{{11\pi }}{5}\)
Bài 11 :
Hoàn thành bảng sau:

Bài 12 :
Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:
|
Số đo theo độ |
0° |
? |
45° |
60° |
? |
120° |
? |
150° |
180° |
|
Số đo theo rad |
? |
\(\frac{\pi }{6}(rad)\) |
? |
? |
\(\frac{\pi }{2}(rad)\) |
? |
\(\frac{{3\pi }}{4}(rad)\) |
? |
\(\pi (rad)\) |
Bài 13 :
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết \(\widehat {AOB}\) có số đo bằng bao nhiêu độ.
Bài 14 :
Đổi số đo của các góc sau đây sang radian
a) \(38^\circ \)
b) \( - 115^\circ \)
c) \({\left( {\frac{3}{\pi }} \right)^\circ }\)
Bài 15 :
Đổi số đo của các góc sau đây sang độ:
a) \(\frac{\pi }{{12}}\)
b) -5
c) \(\frac{{13\pi }}{9}\)
Bài 16 :
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = {\left( {\frac{1}{{60}}} \right)^\circ }\) của đường kinh tuyến (Hình 17). Đổi số đo \(\alpha \) sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilomet, biết bán kính trung bình của Trái Đất là 6371km. Làm tròn kết quả đến hàng phần trăm.
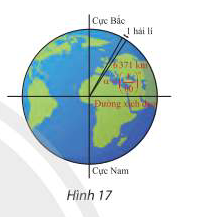
Bài 17 :
Góc có số đo \({75^o}\) bằng bao nhiêu radian?
-
A.
\(\frac{{5\pi }}{{12}}\)
-
B.
\(\frac{{7\pi }}{{12}}\)
-
C.
\(\frac{\pi }{2}\)
-
D.
\(\frac{\pi }{6}\)
Bài 18 :
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
-
A.
\({30^o}\)
-
B.
\({45^o}\)
-
C.
\({60^o}\)
-
D.
\({90^o}\)
Bài 19 :
Nếu một góc lượng giác có số đo là \(\alpha = - {45^{\rm{o}}}\) thì số đo radian của nó là
-
A.
\( - \frac{\pi }{2}\)
-
B.
\( - \frac{\pi }{4}\)
-
C.
\(\frac{\pi }{4}\)
-
D.
\(\frac{\pi }{2}\)
Bài 20 :
Khẳng định nào sau đây là đúng?
-
A.
\(\pi \) rad = \({1^o}\)
-
B.
\(\pi \) rad = \({60^o}\)
-
C.
\(\pi \) rad = \({180^o}\)
-
D.
\(\pi \) rad = \({120^o}\)
Bài 21 :
Đổi số đo của góc \( - \frac{{3\pi }}{{16}}\) rad sang đơn vị độ, phút, giây.
-
A.
33°45'
-
B.
−29°30'
-
C.
−33°45'
-
D.
−32°55'
Bài 22 :
Đổi số đo của góc $\alpha = 30^\circ $ sang rađian.
-
A.
\(\alpha = \frac{\pi }{2}\)
-
B.
\(\alpha = \frac{\pi }{4}\)
-
C.
\(\alpha = \frac{\pi }{6}\)
-
D.
\(\alpha = \frac{\pi }{3}\)
Bài 23 :
Hoàn thành bảng sau

Bài 24 :
Đổi số đo góc \(\alpha = {105^0}\) sang rađian ta được:
A.\(\alpha = \frac{{5\pi }}{8}\).
B. \(\alpha = \frac{\pi }{8}\).
C. \(\alpha = \frac{{7\pi }}{{12}}\).
D. \(\alpha = \frac{{9\pi }}{{12}}\).
Bài 25 :
Góc có số đo \(\frac{{7\pi }}{4}\) radian bằng bao nhiêu độ?
-
A.
\({315^o}\)
-
B.
\({45^o}\)
-
C.
\({345^o}\)
-
D.
\({275^o}\)
Bài 26 :
Đổi số đo của các góc sau đây sang radian:
a) \({15^0}\);
b) \({65^0}\);
c) \( - {105^0}\);
d) \({\left( {\frac{{ - 5}}{\pi }} \right)^0}\).
Bài 27 :
Đổi số đo của các góc sau đây sang độ:
a) 6;
b) \(\frac{{4\pi }}{{15}}\);
c) \( - \frac{{19\pi }}{8}\);
d) \(\frac{5}{3}\).
Bài 28 :
Đổi từ rađian sang độ với số đo $ - \frac{{13\pi }}{5}$ ta được
-
A.
$36^\circ $.
-
B.
$468^\circ $.
-
C.
$ - 468^\circ .$
-
D.
$486^\circ $.
Bài 29 :
Trong các mệnh đề sau, mệnh đề nào là sai:
-
A.
$120{^\circ} = \dfrac{2\pi}{9}\,\,\text{rad}$.
-
B.
$250{^\circ} = \dfrac{25\pi}{18}\text{rad}$.
-
C.
$135{^\circ} = \dfrac{3\pi}{4}\text{rad}$.
-
D.
$300{^\circ} = \dfrac{5\pi}{3}\,\text{rad}$.


















Danh sách bình luận