Đề bài

Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:

• A. ABCD là hình thang cân
• B. AC = BD
• C. BC = AD
• D. Tam giác AOD cân tại C.

Phương pháp giải

Chứng minh ABCD là hình thang cân.

Lời giải của GV Loigiaihay.com

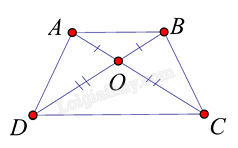
Ta có: \(OA = OB;OC = O{{D}} \Rightarrow OA + OC = OB + O{{D}} \Rightarrow AC = B{{D}}\)

Hình thang ABCD (AB //CD) có AC = BD nên ABCD là hình thang cân

Suy ra: BC = AD

Đáp án : D

Mở rộng

◦ Khái niệm hình thang: Hình thang là tứ giác có hai cạnh đối song song. Trong hình thang ABCD với AB // CD, AB và CD là hai cạnh đáy. Hai cạnh còn lại (AD và BC) là các cạnh bên.

◦ Khái niệm hình thang cân: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

◦ Tính chất của hình thang cân:

▪ Trong hình thang cân, hai cạnh bên bằng nhau.

▪ Trong hình thang cân, hai đường chéo bằng nhau.

◦ Dấu hiệu nhận biết hình thang cân: Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.